授業力をみがく

平行移動に関する理解の素地形成�A

平行移動に関する理解の素地形成〜比例や一次関数の学習で表づくりを工夫する〜

茨城大学教育学部　助教　荻原 文弘

（前回の内容はコチラ）

3 式と表、グラフを関連付ける （続き）

　個人追究や席を立って自由に級友と話しあう活動の際には、追究状況に応じて、｢yがxに比例する｣と｢y−2がx＋1に比例する｣の意味の違いや性質の違いを考えさせたり、ヒントとなる空欄がある表を提示したりしながら追究を進めさせると、生徒は表2を完成させました。

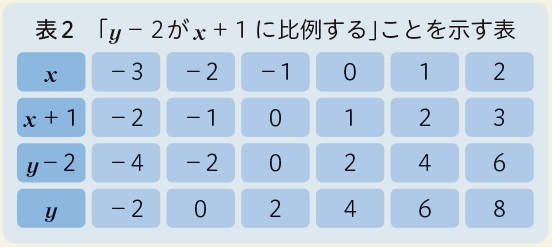
　その後、表の x＋1とy−2の欄を観察しながら、比例の性質が表れていることを確認し、｢y−2がx＋1に比例する｣の意味に関する理解を深めていました。また、全体追究の場面では、生徒から意見｢y＝2x＋4は、y− 4 ＝ 2x とも表せるから、y−4 はx に比例するのでは？｣が出されました。そこで、その意見について他の生徒に問うと、表3を作成して、その意見が正しいことを認めていました。

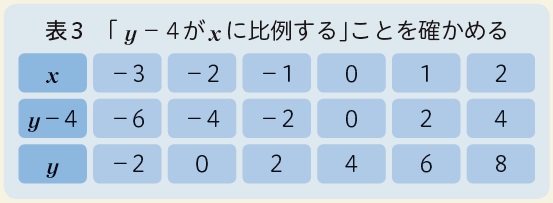
　その後、生徒の興味関心は、この式変形とグラフの関係に移っていきました。y切片がy軸方向への平行移動を表していることを踏まえて、表とグラフを見比べながら、y− 4 ＝ 2x の意味を記述していました。そして、生徒の興味関心は、改めて、y＝ 2xとy＝ 2x＋4のグラフにおける位置関係に移っていきました（図2）。

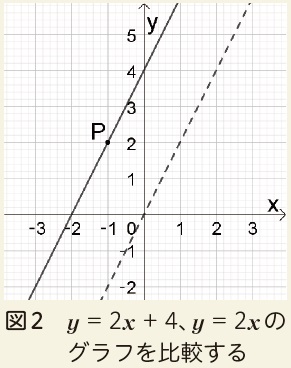
　生徒の中には、表2の点P( − 1,2) に着目し、｢y＝ 2x＋ 4 上の点をx軸方向に1、y軸方向に−2だけ移したら、yはxに比例｣と記述する生徒も見られました。
　さらに、教師により、その他にも変形できるか調べるように促すと、次のような式変形が次々と生まれ、表を用いたりして、比例の関係が確かめられていました。
・y＝ 2(x＋ 2)　　　・y＋ 2 ＝ 2(x＋3)　
・y− 6 ＝ 2(x− 1)　ほか
　これらの一連の活動は、グラフの平行移動に関する理解を促す素地形成の場となり得ます。



【参考文献】
高橋陽一郎 ほか（2011）「数学�T」啓林館
岡本和夫・森杉馨・佐々木武・根本博 ほか（2015）「未来へひろがる数学1〜3」啓林館

--------------------------------------

荻原 文弘（おぎはら ふみひろ）（茨城大学教育学部 助教）

長野県出身。東京理科大学理工学研究科修了。長野県内の私立中高一貫校において，28年間教鞭を執った後、2019年度より現職。

この原稿は、「学びのとびら」2020年春号に掲載された内容を一部改変したものです。

次回配信予定日：6月29日

記事一覧に戻る

アンケート