授業力をみがく
観測データから惑星の楕円軌道を描く授業の試み
岐阜大学教育学部 教授 河崎 哲嗣
普段の授業の中では、数学や理科などの教科書に描かれている内容を融合させて、いろいろな考え方ができる教育内容を構築することにも、当時の私は意識しておりました。大阪教育大学の教授だった藤井先生の論文(1986)の中に、「中学校から高校までの関数や微分・積分では、グラフや図形を描き、面積・体積を求め、方程式の解の個数を求めるような問題を形式的に解いているだけである」と指摘されています。微分は一次関数によるグラフの局所近似(局所的な変化)で、積分は一次関数のグラフを無限につないで変化を再現する(微小な要素の集まり)のはずなのです。続いて「高校数学(微分積分)の教材が、Science(特に力学)を目指していない。万有引力の法則から惑星の楕円軌道を導くべきである。高校数学における楕円は、自然界となんの関連もないし、放物線も運動ではない」と提言されています。
SSHの数学授業を担当していたこともあり、全国の数学者や数学教育関係者の方々から期待を込められて教育実践をすることになったことがありました。志やレベルの高い授業づくりには自信がなくて、とにかく「高校までの数学の内容を使って、惑星の楕円軌道を表現すれば納得してもらえるだろう」という消極的な気持ちだったものです。まずは高校の物理の先生に支援してもらおうと泣きつき、「中学校や高校の数学は止まっているからなぁ」と笑われ、「地学実習帳(京都地学教育研究会編)の第23章ケプラーの法則の記事を参考にしなさい」と指示してもらいました。それを活用した授業内容をお話ししましょう。
2022年9月27日のコラムで、レーゲンスブルクというキレイな街を紹介させていただき、数学者であり天文学者でもあった住人ヨハネス・ケプラーについて触れましたね。コペルニクスは惑星が太陽を中心に円運動をする地動説を称え、その説を基にして、天文学者のティコ・ブラーエは、精密な天体観測を数十年続けてデータを収集しておりました。残念なことに彼にはそれらを分析するだけの数学の力量がなく、この宝の山を上手に持ち逃げするような怪しい人物達からも距離を置いていたのです。そして、高度な数学の知識を持つケプラーに出逢い、人としての信頼を彼に抱き、助手としてその観測資料を渡して、分析させたのでした。それで「惑星は楕円運動をしている」という法則を発見したと言われています。法則の発見ですから、その時点ではまだ一般性が認められたわけではありません。やがてニュートンが「万有引力の法則」という数学を用いて証明をしました。この三者のバトンリレーは、ビッグデータを使って新たな発見をする現代社会の発展に通ずるものがあります。ティコ・ブラーエは「価値のあるデータを収集」、ヨハネス・ケプラーは「数学の知識でデータを分析して原因追究をし、法則を発見」、アイザック・ニュートンは「数学による一般性を証明して、新しい科学への導きをする」という構図です。これを例に、子どもたちが行う探究が全てを網羅する必要もなく、活動をしている現在地がどのような位置にあり、しかもそれだけでも十分な価値があることを示してあげれば良いのではないでしょうか。
さて、3つあるケプラーの法則のうちの第一法則は「惑星は、太陽を1つの焦点とする楕円軌道を描く」です。それを当時の人物がどのようにして法則を見つけたかを、同じ情景をイメージして、数学の知識を使って描こうと考えました。
理科年表(国立天文台編)には、地球と太陽を結ぶ直線に対しての水星の最大離角が起きる年月日と角度のデータが載っています。つまり、地球と太陽を結んだ直線に対して、東方離角は太陽に向かって左側、西方離角はその右側にできる角度を表します(図1、図2)。そして、この角度が最大となる時のデータだけを集めて描画をするのです。水星が見える直線の部分を太線にして幾つも描き足していきますと、太陽を1つの極(焦点、中心)とする楕円(円もその1つ)が浮かび上がって見えてきます(図3)。
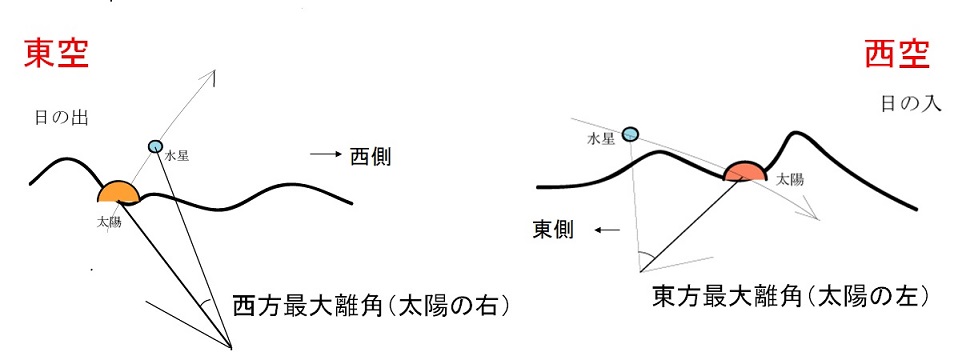
図1 実際の観測イメージ
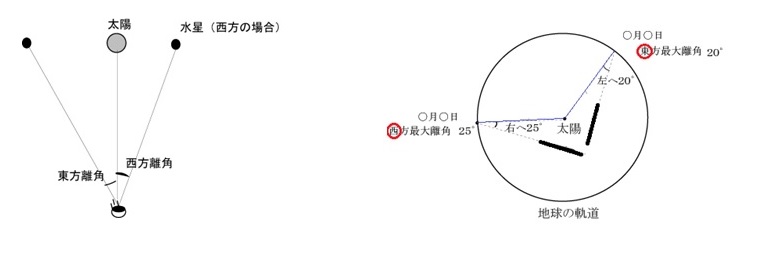
図2(左) 視点と水星を結ぶ直線 / 図3(右) 視点-水星間の直線の描画記録の仕方
実際に理科の先生が毎年手に入れておられる「理科年表」をお借りして、水星の最大離角のデータを使って、次の盤面(図4)に水星と地球(視点)を結ぶ直線(図の太線)の何本かを描画してみてください。
その原理に従って、関数グラフソフトで表してみますと、楕円軌道が浮き上がることを既にケプラーは気づいていたのかもしれませんね。(図5)
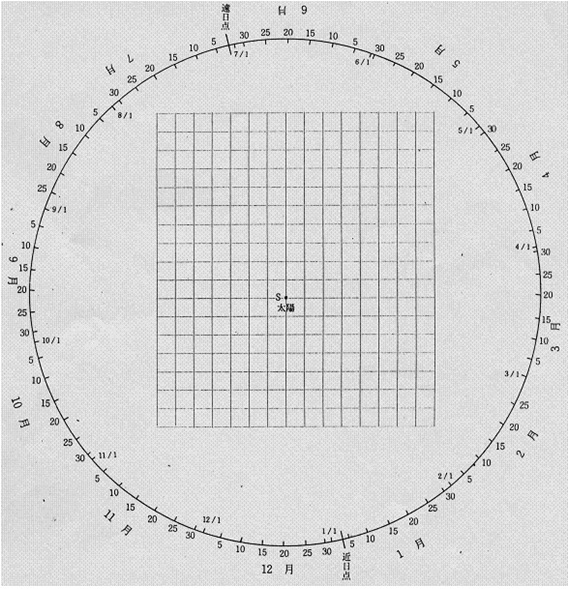
図4 水星軌道を記録する盤面:地学実習帳(京都地学教育研究会編)より抜粋
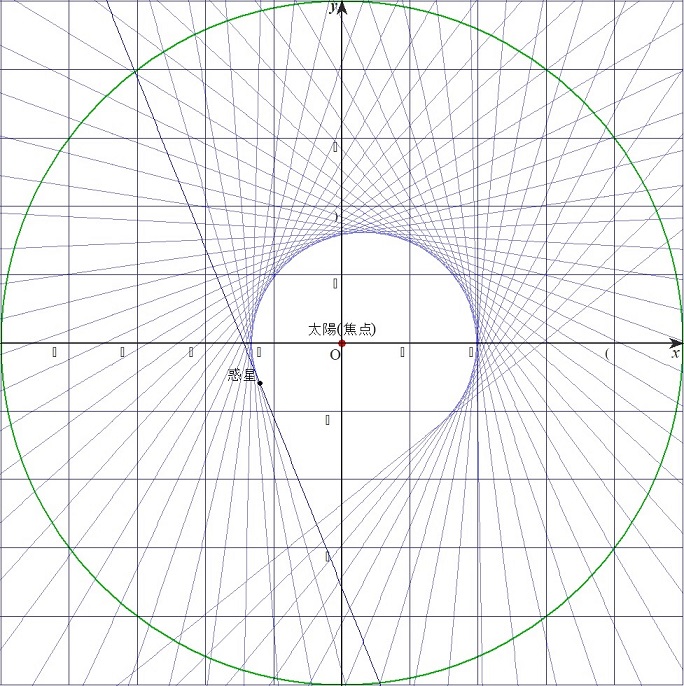
図5 直線の包絡線による浮かび上がる楕円形(Grapesを利用)
この包絡線関連は、高校の数学ⅠⅡの問題として扱われますが、中学生には難しいものです。参考として興味があれば、以下のような問題を解いてみれば、楕円や円の数式が表れます。

これで「惑星運動は楕円軌道をする」ことを示せたと、当時ホッと胸を撫で下ろしたのですが...(次回に続きます)
--------------------------------------
河崎哲嗣(かわさき てつし)
1964年生まれ
数学科教諭として、23年間京都府立高等学校・京都教育大学附属高等学校に勤務
2002年 京都教育大学大学院教育学研究科(修士課程)修了
2016年 大阪大学人間科学研究科博士後期課程修了
2016年 博士(人間科学)大阪大学
現 職 東海国立大学機構 岐阜大学教育学部教授
専 攻 数学教育学,教育工学,国際遠隔協働学習,STEAM
アンケート
よろしければ記事についてのご意見をお聞かせください。
Q1またはQ3のいずれか一方はご入力ください。

