授業力をみがく

平行移動に関する理解の素地形成�B

平行移動に関する理解の素地形成〜比例や一次関数の学習で表づくりを工夫する〜

茨城大学教育学部　助教　荻原 文弘

（前回の内容はコチラ）

4 数学�T｢二次関数｣の学習・指導

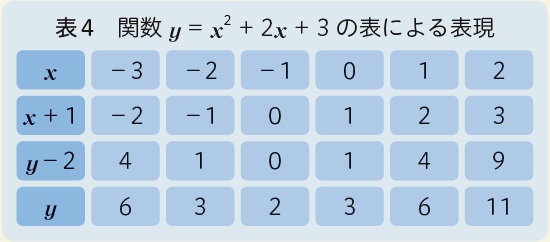
　実際、数学�T｢二次関数｣では、例えば、関数 y＝x^2＋2x＋3 のグラフの追究において、変形式 y−2＝ (x＋ 1)^2 と表4、y＝ (x＋ 1)^2 ＋ 2 とy＝x2のグラフをかき、表でグラフ上の点を読み取りながら平行移動の様子を観察する活動が、生徒の発想から自然に営まれていました。

　｢放物線 y＝ax^2 をx軸方向にp、y軸方向にqだけ平行移動した放物線が y＝a(x−p)^2＋q である｣の理解を促すためには、｢y＝a(x−p)^2＋q上の点を戻したらy＝ax^2の関係になる｣ことを納得させる必要があります。そのためにも，教師は生徒の実態を踏まえて様々な手立てを用意しなければなりません。
　なお，上記の活動の後で紹介した解釈｢負の方向に移動するのは座標軸であり，そのためグラフは相対的に正の方向に移動するようにみえる」は，｢引けば負の方向へ移動する｣という感覚にも邪魔されず，すべての生徒が違和感なく納得する考え方でした。

【参考文献】
高橋陽一郎 ほか（2011）「数学�T」啓林館
岡本和夫・森杉馨・佐々木武・根本博 ほか（2015）「未来へひろがる数学1〜3」啓林館



--------------------------------------

荻原 文弘（おぎはら ふみひろ）（茨城大学教育学部 助教）

　長野県出身。東京理科大学理工学研究科修了。長野県内の私立中高一貫校において，28年間教鞭を執った後、2019年度より現職。

この原稿は、「学びのとびら」2020年春号に掲載された内容を一部改変したものです。

記事一覧に戻る

アンケート