授業力をみがく

観測データから惑星の楕円軌道を描く授業の試み�A

（前回の内容はコチラ）

岐阜大学教育学部　教授　河崎 哲嗣


前回は、多くの観測データからケプラーの第1法則の発見確認までの様子をお示ししました。さらにその地学実習帳では、水星軌道の盤面を用いて、第２法則「惑星と太陽とを結ぶ線分が単位時間に描く面積は一定である（面積速度一定の法則）」や第３法則「惑星の公転周期Tの2乗は、楕円軌道の半長軸aの3乗に比例する」についても確認発見する作業ができるようになっています。

小学校４年生理科から「太陽の動き」として影の様子を扱っていますね。太陽は焦点の1つであって、本来はその太陽を焦点として地球が運動しているのに、それを実感させることはなかなか難しいものです。場面によって「天動説」を上手く活用して「地動説」に注入しなければ、上手に伝わらない難しさがあります。周辺の子どもたちに一度尋ねてみてください。依然、地球中心の「天動説」で理解が止まっている子も多くいます。
　地学実習帳での作業は「実験・実習・観測」によって得られた多くのデータを「帰納的」に証明した例です。水星以外のすべての惑星についても同じであるかどうかについては示されていません。皆さんもご存じのこの法則は普遍的なものであり、その「演繹的な証明」を与えたのがアイザック・ニュートンの「万有引力の法則」です。数学の力を用いて「定数係数型2階線形微分方程式」を解けば、これらケプラーの法則を一度に証明してしまいます。
　他の単元との比重や授業時間数等との加減で仕方ないのですが、高校数学は勿論のこと、高校物理でも紹介程度で済まされています。大切なことは「科学者・技術者」を目指そうと思う子どもたちが、背景や事実を認識した上で成長してほしいということです。これを読んでくださっている先生方には、長い年月を掛けてでも良いのでゆっくりと、以下のような微分方程式

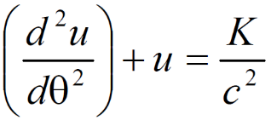
から、高校数学の

への導きに挑戦してみてください。

　ところでその後、授業でどのように扱ったのかその一端を紹介いたしましょう。
まず、多くの生徒たちは間違った「認識」を持ち続けているのではと疑いました。次の2つの画像を比べて、どちらが惑星運動なのか尋ねてみたのです。

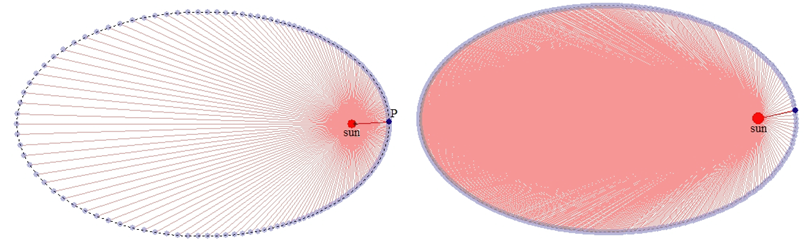
　見事に左図の角速度一定の運動を選択する生徒が多かったです。この生徒たちの「つまずき」の原因は、x，y軸の【直交座標】上において、中心を原点（2焦点を重ねる）とする等速円運動で捉えているということ。そして、面積の求積の考え方が根底に浸かっています。残念ながら【極座標】上の運動の様子や面積の求積については、高校での扱いにも及んでいないからです。
　「ハッ！！」と驚いて、彼らの思い込みの間違いに気づくことがとても重要ではないでしょうか。今学習している数学は「自然科学を解明することにあまり役に立っていないのでは？」と。そして、理科で学ぶ【ex「バネによって拘束された物体の運動」「インダクタンスLと容量Cを連結した回路」】のような振動の微分方程式(一般の単振動を表す)から繋がるであろうこの壮大な法則を、先生方ももう一度認識していただけたら幸いです。
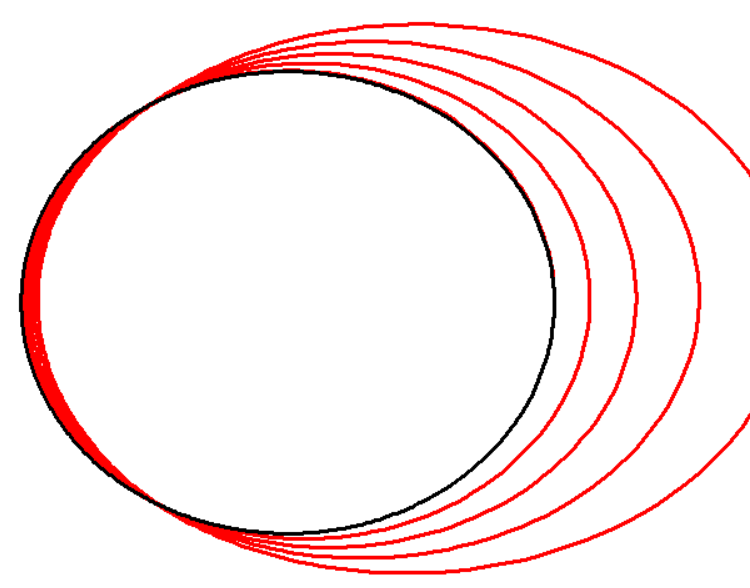
　授業では、その時その時の物体の運動の様子を表現した微分方程式の解法に多く触れるなんてことは難しいものですね。「積み重ねていくと、未来の状況を表現することができる」考え方が重要なのであって、その原理を視覚化して実感させるには、「数値解析法」を用いた「解曲線」で表現してみると効果的です。その手法として、25年前のことになりますが、「プログラミング」を扱った授業を実践しました。
　以下のソースは、オイラー法で十進BASICを使って、微分方程式を解いています。

十進BASIC

　焦点付近で点が加速している描画の様子をじっくり観察して確認をしてみてください。また、dsの数値を色々と変えてみると、解曲線が楕円に収束したり、双曲線などの2次曲線も浮かんできます。さらに、ルンゲ・クッタ法を用いれば、もっと精度が良くなります。今度はScratchを使って表現すると面白いでしょう。ぜひこれらを参考にしてみてください。

記事一覧に戻る

アンケート