今知りたい授業のワンポイント

大きな数のしくみ・計算

■位取り記数法

　十進位取り記数法は、次の2つの仕組みを基本的な原理としています。
　1．それぞれの単位の個数が10個になると、新しい1つの大きな単位に置き換える（十進数の仕組み）。
　2．それぞれの単位を異なる記号を用いて表すかわりに、数字をかく位置の違いによって表す（位取り記数法の仕組み）。

　教科書p.60では、この位取り記数法を用いれば、どのように大きな数でも、0、1、2、3、4、5、6、7、8、9の10種類の数字で表せることを、13桁の数を観察したりつくったりする活動を通してとらえさせるようにしています。
　「どんな大きさの数でも」という観点からすれば、13桁だけでなく、いろいろな例を取り上げて帰納的な結論を導かせるほうが望ましいでしょう。ポイントは、10種類の数字を使って10桁以上の大きな数をつくることができると気づかせることです。教科書では最小限必要な桁数として13桁にしています。

■末尾の0を処理して積を求める計算

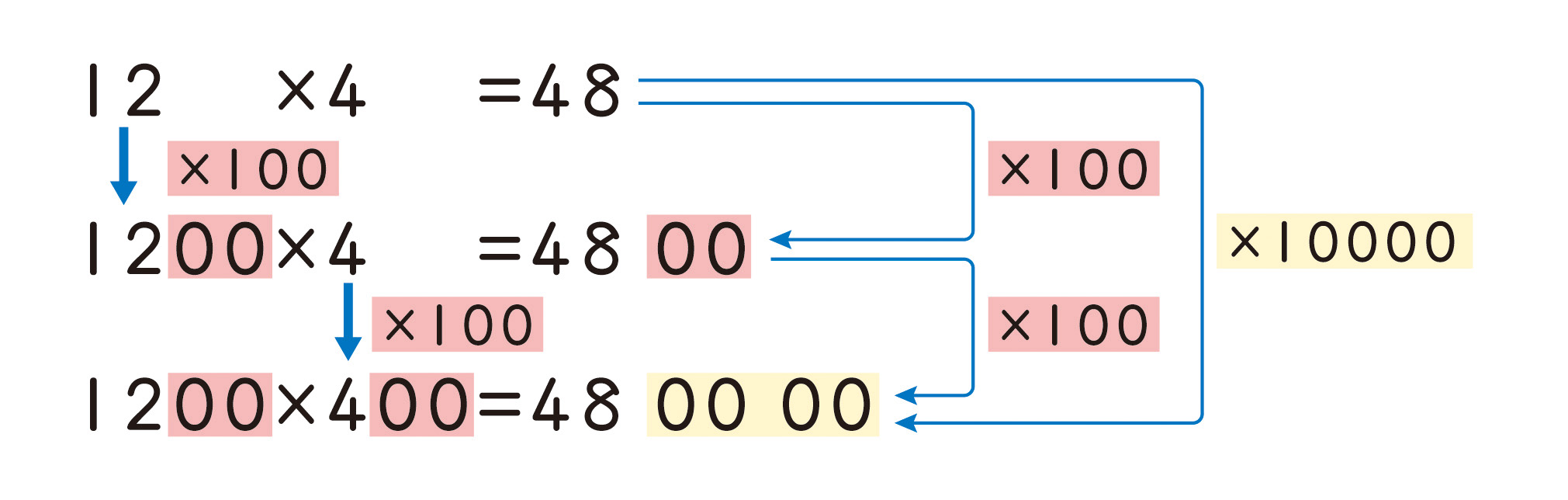
　教科書p.19では、第3学年で学習した（2位数）×（2位数）の計算をもとに、末尾の0を処理する方法を考えさせます。
　1200は12の100倍、さらに400は4の100倍となっていることから、1200×400の計算は、12×4の積の100倍の100倍、すなわち10000倍（1万倍）であることに気づかせたいものです。
　その上で、末尾に0のついた数の計算を形式的に処理する方法として、0をはずした数の計算をした後で、はずした個数だけ0をつければよいことをわかるように指導しましょう。
　また、p.19のように、「100倍の100倍は1万倍」を理解すれば、末尾の0をつけなくても「48万」のように「万」を使った表記が可能であることも知らせておくようにします。

1.1億をこえる数（教科書p.10〜22）

記事一覧に戻る

アンケート