授業のワンポイント

作図・おうぎ形

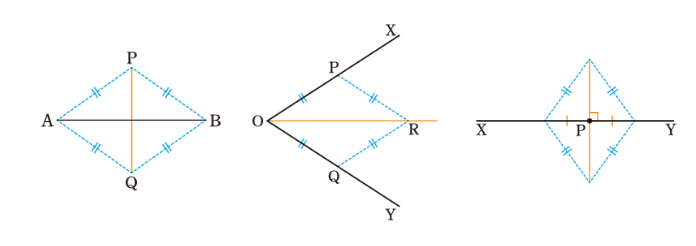
■ひし形の対角線の性質を使う作図

　角の二等分線，線分の垂直二等分線，垂線の作図方法は，対称性に着目すれば同じものと見ることができます。いずれも，2つの円が，中心を結ぶ直線に対して線対称であることを用いています。
　このとき，半径が等しい2つの円の交点と2つの円の中心を結ぶと，ひし形になります。つまり，角の二等分線，線分の垂直二等分線，垂線がすべて，小学校で学んだひし形の対角線になっています。だから，作図の根拠として，ひし形の対角線の性質を使っています。
　コンパスを使ってひし形をかくことができない生徒は意外に多いため，かいたひし形に対角線を引かせ，ひし形の性質をすべて引き出して，ひし形の理解を深めましょう。

■おうぎ形の中心角の求め方

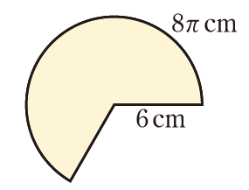
　教科書p.173の例題1ような，弧の長さと半径（r）がわかっているおうぎ形の中心角（x）を求める問題の解き方として，次の3つの方法が考えられます。

（ア）弧の長さの比と中心角の比が等しくなることから，次の比例式をつくる。

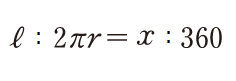
（イ）弧の長さを求める公式を使って，次の方程式をつくる。

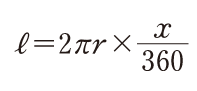
（ウ）全円周に対するおうぎ形の弧の長さの比の値を360°にかけて，次の式で求める。

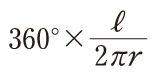
　教科書では，（ア）の方法を主なる解答とし，（イ）の方法を別解として取り上げています。その理由は，ここまでに「1つの円では，おうぎ形の弧の長さは，その中心角の大きさで決まる」ことを学習しているので，中心角の比や比の値を用いる（ア）や（イ）の方法が自然だからです。
　（ア）〜（ウ）のどれでなければならないということはなく，生徒の実態に応じて，理解できる方法を選択することが大切です。

［5章］平面図形　
2節　移動と作図
3節　円とおうぎ形（教科書p.153〜177）

記事一覧に戻る

アンケート