授業のワンポイント

√の導入・意味理解

■記号√の導入

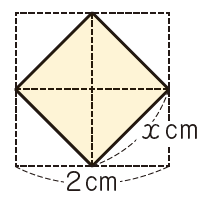
　教科書p.41では，面積が2cm^2の正方形の1辺の長さを表す数の存在を確認するとともに，2乗してちょうど2になる数は，今まで学んだ数にはないことを実感させ，このような数を表す記号として，√を導入します。
　また，√2は2乗すると2になる数のうち，正の方を表し，2つある2の平方根のうち負の方は，これに−をつけて−√2と表されることをおさえます。

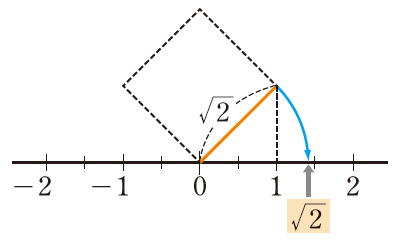
　この√2や−√2は，これまで知っている数では言い表せない数ですが，教科書p.41の図のように，コンパスでその長さをうつしとることで，数直線上に表される1つの数であることが実感されます。
　また，この記号で表した√2と−√2も，p.40の数と同様に，その絶対値が等しいことが，数直線から視覚的にわかります。

■√のついた数の意味理解

　−√2や√3など，根号のついた数を具体的な数と捉えずに，形式的な記号だと捉えてしまう生徒もいます。
　そこで教科書p.38〜39の活動では，正方形の1辺の長さとして現れることを意識づけ，教科書p.41でそれを数直線にうつすことにより，平方根が数直線上の数であることを確認します。
　また，教科書p.44では，そのおよその値を，小数を用いて表現し，平方根の数としての存在を意識させるように配慮しています。

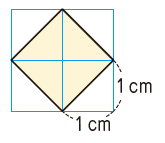
面積2cm^2の正方形の1辺の長さは√2cm。√2cmはおよそ1.4。

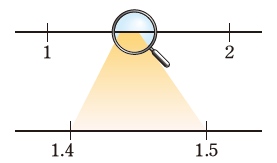
1.4^2＝1.96，1.5^2＝2.25で，1.96＜2＜2.25だから，1.4＜√2＜1.5

［2章］平方根
1節　平方根（教科書p.38〜49）

記事一覧に戻る

アンケート