授業のワンポイント
変域外のグラフの表し方
■変域外のグラフの表し方
変域のあるグラフをかくときの変域外の表し方については,破線で表す場合もあれば全く表記しない場合もあり,特に表し方の決まりはありません。
この教科書では,変域外の部分を破線で表している場合もあります。これは,方眼がないところにグラフをかいた場合や,変域の範囲内で軸と交わっていない場合でも,グラフから関数の式がわかるようにするためです。
中学校の関数の指導では,表,式,グラフを相互に関連づけて,2つの数量の変化や対応の特徴を捉えることが大切なので,変域のあるグラフからも式がわかるように,必要に応じて変域外を破線で表しています。
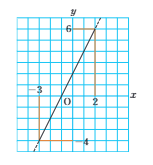
xの変域に制限があるときのyの変域
一方,試験などで「変域のある関数のグラフを書くように指示された場合に,変域外の部分まで含めて破線などでかかないと不正解かどうか」ということについては,本来,グラフは,視覚的に表すことによって,関数の変化の様子をとらえやすくするためにかくものであり,教科書はその姿勢を養うためにグラフの利用を取り上げているので,それぞれの場面に応じて変化を捉えるのに支障がないグラフがかかれていれば,それでよいと考えています。もちろん,変域の範囲内だけでしかかかれていないグラフでは,正しいかどうかの判断がつかない場合もあるので,必ず範囲外の部分も破線でかくように指導されることを否定するものではありません。
いずれにしても,表,式,グラフを相互に関係づけ,関数関係を見いだし,表現し,考察することを通して,関数的な見方や考え方を養うという関数指導のねらいに沿った指導や評価をおこなうことが大切です。
[3章]一次関数
1節 一次関数とグラフ(教科書p.60〜78)
アンケート
よろしければ記事についてのご意見をお聞かせください。
Q1またはQ3のいずれか一方はご入力ください。

