授業のワンポイント

展開の公式

■（x＋a）（x＋b）の展開

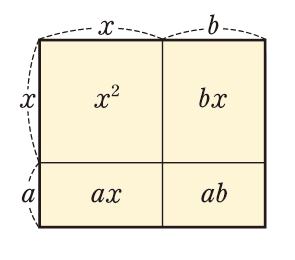
（x＋3）（x＋5）のように，具体的な一次式の積を展開し，xの係数と数の項に着目することで，公式を帰納的に類推させます。その後に，一般的に公式となるものを導かせるとよいでしょう。また，（x＋a）（x＋b）を表した面積図も公式の意味を理解する手助けになるので，活用しましょう。
　教科書p.16の問1では，計算する式のa，bにあたる数が何であるのかを確認しながら，
「xの係数は，たして〜」
「数の項は，かけて〜」
のように，はじめのうちは，口頭で展開の練習をさせることも有効です。

■（a＋b）^2，（a−b）^2の展開

　（a＋b）^2は（a＋b）（a＋b）であることを確認し，前項の方法で展開し，公式を導きます。
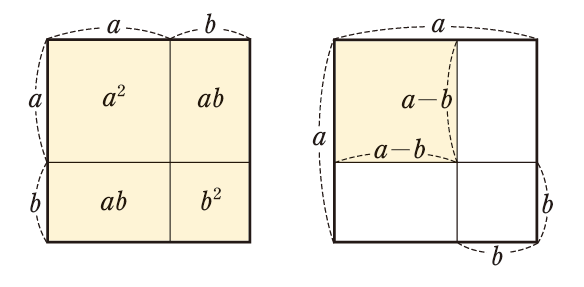
　a＞0，b＞0の場合について，面積図をそろえて2つの平方の公式を表しているので，公式の理解のために活用しましょう。また，（a−b）^2についても，（a−b）（a−b）であることを確認し，公式を導きます。ここでは，　a＞b＞0の場合の図を示しています。
　これらの面積図から，
　（a＋b）^2≠a^2＋b^2
　（a−b）^2≠a^2−b^2
であることがわかります。

■（a＋b）（a−b）の展開

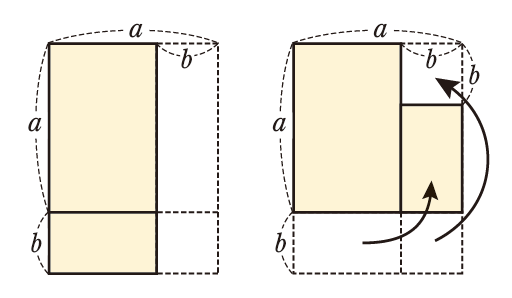
　（a＋b）（a−b）を，分配法則を使って展開し，公式を導きます。面積図をそえて示していますが，公式との対応関係が理解しにくい場合には，実際に紙などを使って考えてもよいでしょう。
　この公式は，
　「和と差の積は2乗の差」
のように記憶させるとよいでしょう。

［1章］式の展開と因数分解　
1節　式の展開と因数分解（教科書p.10〜27）

記事一覧に戻る

アンケート