授業のワンポイント
動く点と面積の変化
■ΔAPDの面積が0になる場合の扱い
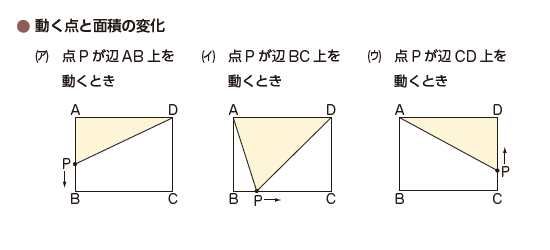
教科書p.88では,ΔAPDの面積の変化を調べています。
このとき問題文にもとづいて厳密に考えれば,点Pが点Aあるいは点Dと一致するとき,すなわちx=0のときには,三角形はできず,そもそも三角形がないのだから面積は考えることができない,ということになります。
つまり,対象となる図形を三角形に限定することで,三角形ができないところは変域に含めないという考え方です。
一方,こうした事態を避ける1つの方法として,ΔAPDとせずに,AP,PD,DAで囲まれる図形とすることが考えられます。
すると,点Pが点Aあるいは点Dと一致するときには,線分ADができるから,AP,PD,DAで囲まれている図形の面積は0であるとまとめることができます。
つまり,できる図形を限定しないことで,点が動く範囲すべてを変域とするという考え方です。
いずれの考え方も重要であり,どちらでなければいけないということはありません。学級の生徒の実態や先生ご自身の考え方に従って,どちらの方針で指導するのがよいかご判断ください。
なお,試験などの問題として出題する場合には,あらかじめ点Pが点Aあるいは点Dと一致するときを変域から除いたり,点Pが点Aあるいは点Dと一致するときには三角形はできないものの,線分の面積を0と考えて変域に含めたりすることなどを問題文の中で示すとよいでしょう。
[3章]一次関数
3節 一次関数の利用(教科書p.84〜93)
アンケート
よろしければ記事についてのご意見をお聞かせください。
Q1またはQ3のいずれか一方はご入力ください。

