授業力をみがく
子どもができることを大切にした指導(2)
文教大学教育学部 教授
永田 潤一郎
3 円の性質に関する証明と説明
次の問題1と問題2をみてください。どちらも第3学年の内容である円の性質に関する問題で,問題1は,∠B=50°,∠D=30°の場合に成り立つ事柄を説明する問題。円周角の定理の適用問題として求答式で扱う先生もいるでしょうが,この問題のように説明を求める問題とすることも可能です。問題2は,その性質がいつでも成り立つことを証明する問題。証明の練習として取り上げている先生もいるのではないでしょうか。根拠を明らかにしながら筋道立てて推論し説明するという意味で,どちらの問題も論理的に考察し表現する能力を問う問題であり,根拠となる図形の性質も同じですが,子どもの解答状況に違いが出るでしょうか。
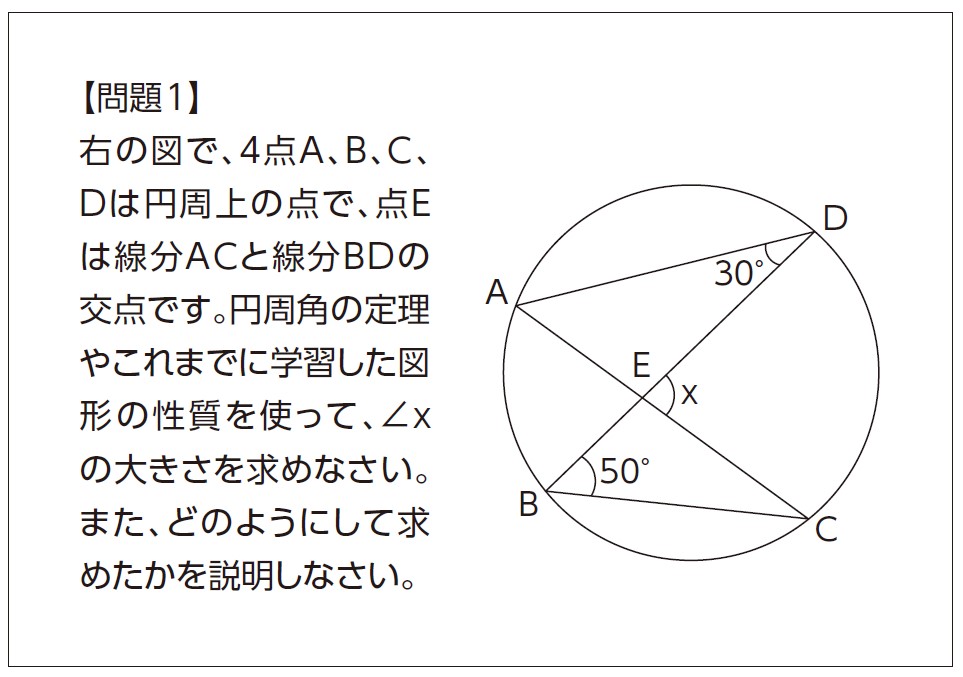
〔問題1〕
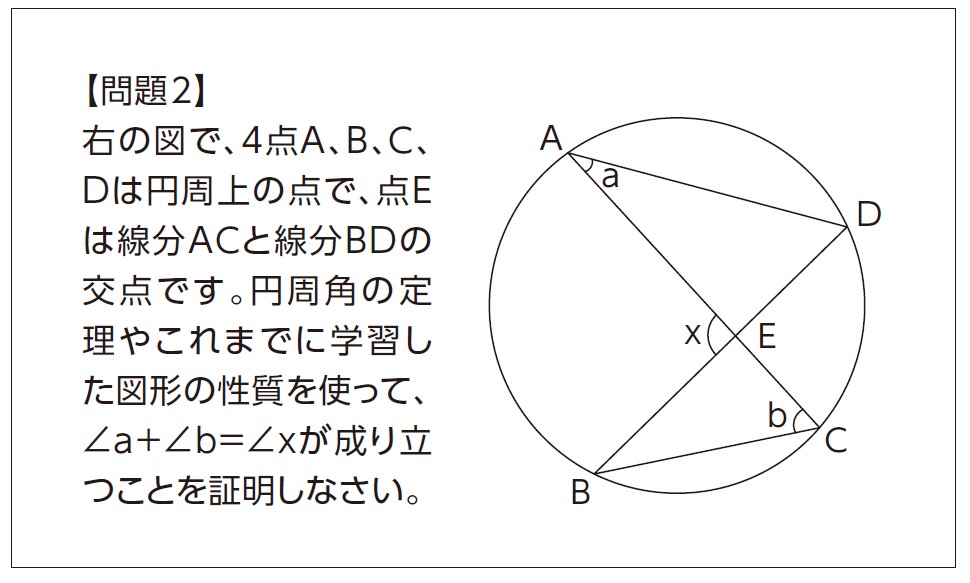
〔問題2〕
ある公立中学校の子ども135人にこの問題を解いてもらったところ,正答率は,問題1が約72%であったのに対し,問題2は約59%で約13ポイント下回りました。なお,問題1の正答とは,∠xの大きさを正しく求め,説明もできていることを意味します。説明では単に角の大きさを求める手順だけではなく,根拠となる事柄を明記するよう事前に指示しています。無解答率は,問題1が約7%であったのに対し,問題2は約15%と2倍程度に達しました。こうした結果は,問題1が∠xの大きさを求めた上で,それを求める思考の過程を説明するという形式になっていることと関係していると考えられます。
また,問題1は正答できたのに,問題2に正答できなかった子どもが全体の約20%いました。この子たちを「証明できないから,論理的に考察し表現できない」といってしまってよいでしょうか。ある意味,充分論理的だと思うのですがいかがでしょう(永田,2014)。
4 できることからはじめてみよう
証明の指導の改善は,「証明ができない」ことを前提に進めることもできるでしょうが,論理的に考察し表現する能力の育成という視点から,「証明はできないが,ある種の説明ならできる」という考え方で検討することもできそうです。問題1のような説明を通じて,根拠を明らかにしながら筋道立てて推論することの意味を理解できるように指導し,その考え方を証明につなげる授業づくりはできないでしょうか。また,思考力・判断力・表現力等の育成という視点から考えた場合,図形の性質がいつでも成り立つことの証明だけにこだわり過ぎず,問題1のような説明も積極的に授業に取り入れることが有効なのではないでしょうか。
こうした「できること」から考える指導の改善は,中学校数学科における他の課題の解決にも活かせると思うのですが,それはまた別の機会に…。
引用・参考文献
・国立教育政策研究所(2012)『全国学力・学習状況調査の4年間の調査結果から今後の取組が期待される内容のまとめ −児童生徒への学習指導の改善・充実に向けて−』教育出版
・文部科学省(2008)『中学校学習指導要領』東山書房
・永田潤一郎(2014)『中学校数学科における論理的に考察し表現する能力の育成について』「文教大学教育学部紀要 第48集」
------------------------------------------------------------
永田 潤一郎先生
1962年東京都出身。千葉大学大学院教育学研究科数学教育専攻修了後,千葉県内の公立高校・国立中学校に勤務。その後,文部科学省初等中等教育局教育課程課で教科調査官として学習指導要領の改訂や評価規準の作成等を担当すると共に,国立教育政策研究所で教育課程調査官・学力調査官として研究指定校の指導や全国学力・学習状況調査の問題作成及び分析等に取り組んだ。千葉県教育庁指導課教育課程室に勤務後,2012年から現職。
この原稿は,「理数啓林 授業力をみがく」に掲載された内容を一部改変したものです。
アンケート
よろしければ記事についてのご意見をお聞かせください。
Q1またはQ3のいずれか一方はご入力ください。

