授業のワンポイント

連立方程式の解の示し方

■連立方程式の解の示し方

　連立二元一次方程式の解の表記は，教科書p.40にもあるように，次の【1】，【2】，【3】など複数の書き方があります。
　xやyの値が明確に表現されているという観点では，解の表記は，【1】，【2】，【3】のどれであっても構いません。

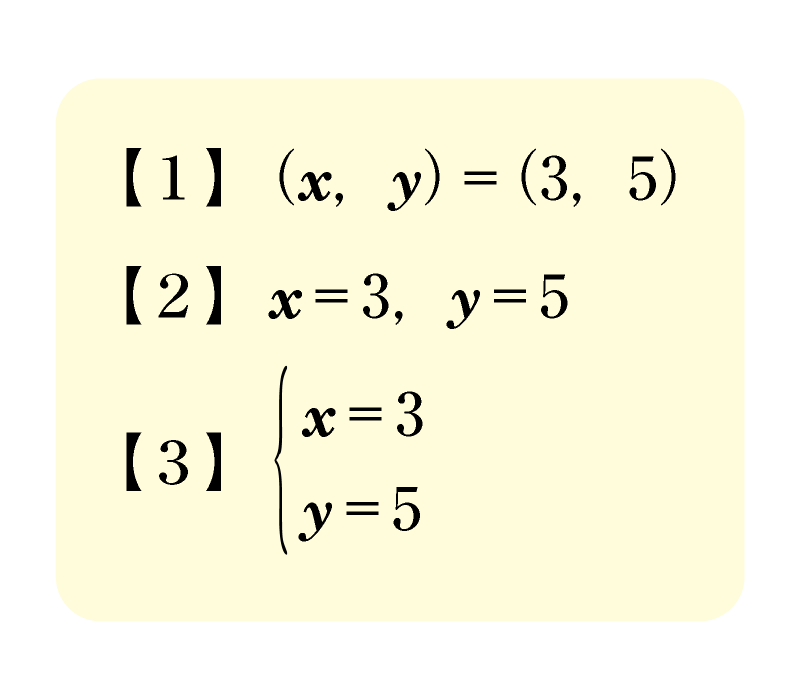
　この教科書では，順序対を用いた【1】の解の表記を採用しています。
　その主な理由は，次の3つです。
・連立二元一次方程式の2つの値の組であることを明確に表せること。
・2直線の交点の座標と連立方程式の解との関連づけがしやすくなること。
・一次方程式や二次方程式を含めた方程式の解の表記の仕方を集合の表記に基づいて統一できること。

■さっさ立て

　教科書p.57で紹介している「さっさ立て」は，江戸時代に中根彦循（なかねげんじゅん）が書いた和算の本「勘者御伽双紙（かんじゃおとぎぞうし）」に書かれています。

　【い】の袋にはいっている碁石をx個，【ろ】の袋にはいっている碁石をy個として連立方程式を立てると，次のようになります。

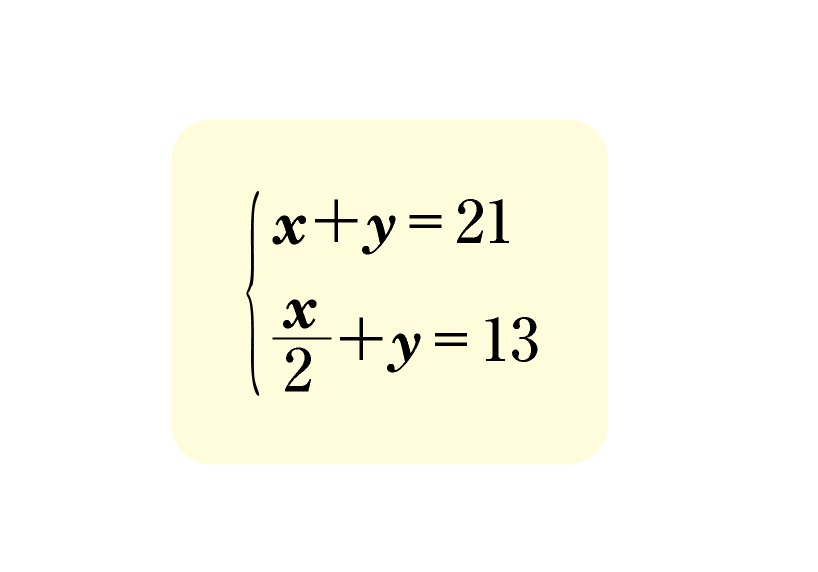
　【い】，【ろ】の袋にいれた回数を，x，yとして解いても構いません。

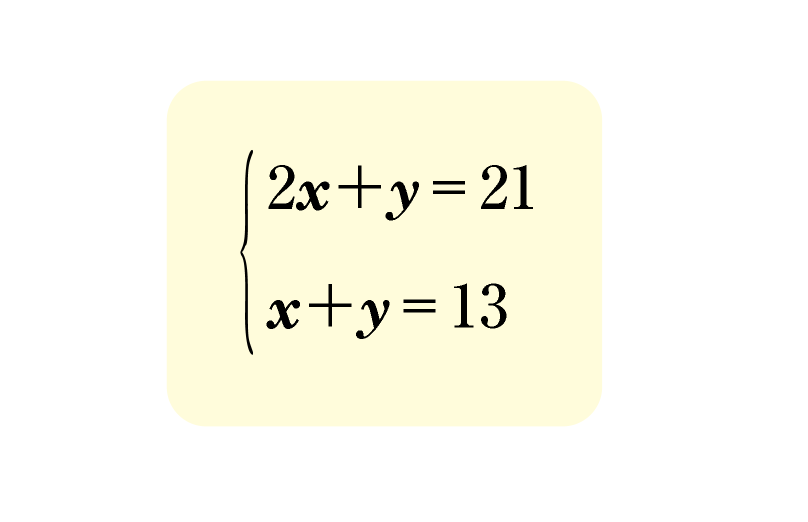
　中根彦循（1701〜1761）は，江戸時代中期の和算家です。著作に「勘者御伽双紙」，「開方盈肭術（かいほうえいじくじゅつ）」「竿頭（かんとう）算法」などがあります。特に，勘者御伽双紙の中で紹介されている「小町算」は，非常に美しいパズルとして，現在でも広く知られています。

【小町算】
　次のように，１から９の数字を順番に並べた数字の間の□に，＋，−，×，÷，空白のいずれかを1つずつ入れて，答えを100にします。
　1□2□3□4□5□6□7□8□9

（解答例）
・1＋2＋3−4＋5＋6＋78＋9＝100
・1＋2＋3−4＋5＋6＋7＋8×9＝100
・1×2×3×4＋5＋6＋7×8＋9＝100
・123＋45−67＋8−9＝100

［2章］連立方程式　
1節　連立方程式
2節　連立方程式の利用（教科書p.34〜57）

記事一覧に戻る

アンケート