授業のワンポイント
図形の性質の証明
■図形の性質の証明
教科書p.33「ひろげよう」は,幅4mの道の面積と,道幅と道のまん中を通る円周の長さの積をそれぞれ計算してくらべる活動です。
まずは,具体的な数で,
(道幅)×(道のまん中を通る円周の長さ)=(道の面積)
の関係を確認しますが,そこから,半径や道幅が変わった場合にも,この関係がいえるかどうかの疑問を生徒自ら考え出すことができれば,p.34の例題2「図形の性質の証明」に自然にはいることができます。
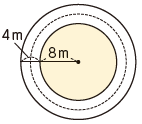
教科書p.33 ひろげよう
p.34の例題2では,p.33で確認した,道幅と道のまん中を通る円周の長さの積が,道の面積に等しいということが,どんな円形の花だんでも,どんな道幅でも成り立つことを,式の計算によって証明します。
S=alであることを証明するためには,左辺と右辺を同じ式で表せばよいこと,そのためには,Sとlを,それぞれa,rを使って表す必要があることを確認します。
証明の途中では,πや分数の形が出てくるので,式の展開や式変形が十分にできるようになっていることが必要です。
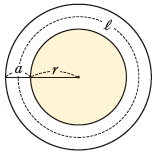
教科書p.34 例題2
そして,p.34の問4では,円形の花だんを正方形の花だんにした場合でも,S=alが成り立つことを証明します。ここでは,S=alとなることを問題で与えていますが,実際に具体的な数値を用いて,S=alが成り立つことを確認させてもよいでしょう。
長方形や三角形などの形に変えた場合について調べてみてもよいでしょう。
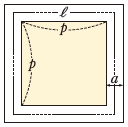
教科書p.34 問4
[1章]式の展開と因数分解
2節 式の計算の利用
1 式の計算の利用(教科書p.30〜39)
アンケート
よろしければ記事についてのご意見をお聞かせください。
Q1またはQ3のいずれか一方はご入力ください。

