授業のワンポイント
変域のあるグラフ・放物線と直線が交わる問題
■変域のあるグラフの端点の表し方
教科書p.118のように,変域のあるグラフのかき方について,変域の端点が含まれるかどうかを,●,○で表すことがあります。
しかし,これは,数学の中で定められた表し方ではありません。このような表記を用いる際は,●と○の意味について,グラフのそばに添え書きをするなど,きちんと断ってから用いる必要があります。
授業の中であれば,図やグラフをかく際に,口頭で宣言しておくだけでも問題はないでしょう。
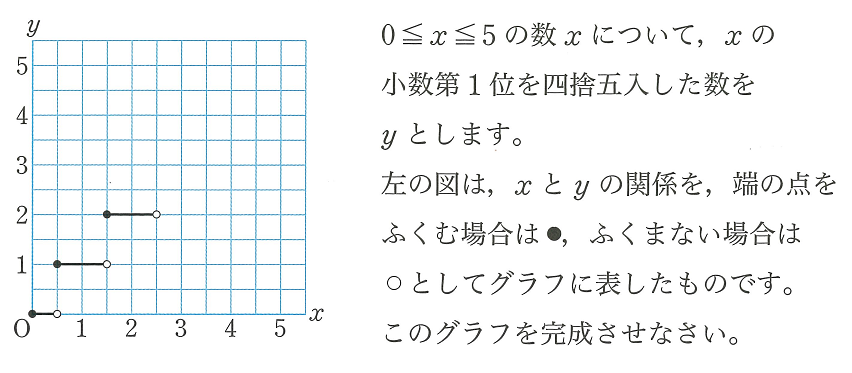
●,○の意味についてグラフのそばに添え書きをする必要がある。
また,教科書の中には,変域のあるグラフを示す際に,端点に●,○を用いていない場合もあります。これは,端点が含まれるかどうかが主眼でない場合には,必ずしも,端点が含まれるかどうかをグラフに示す必要はないという考えにもとづいています。
■放物線と直線が交わる問題の扱い
関数指導のねらいは,本来,2つの数量間の変化や対応のようすをとらえ,その特徴を調べる能力を育てるとともに,関数的な見方や考え方を身につけることです。その手立てとして,表,式,グラフがあるのであって,表,式,グラフがかければそれでよいというわけではありません。
いろいろな関数を学ぶときに,同じように表,式,グラフを関連づけて表現したり,特徴を調べたりすることで,関数的な見方や考え方を一層伸ばしていくことが大切です。
教科書p.119の章末問題7で放物線と直線が交わる問題を扱っており,これは中学校の範囲で解くことができるものです。
これに対し,一次関数と関数y=ax^2の式から二次方程式をつくって交点を求める課題として,教科書「自分から学ぼう編39〜40」の発展「グラフの交点の座標」があります。これは,発展課題,つまり,学習指導要領の範囲外の内容になりますので,生徒の実態に合わせて取り上げてください。
[4章]関数y=ax^2
3節 いろいろな事象と関数(教科書p.110〜119)
アンケート
よろしければ記事についてのご意見をお聞かせください。
Q1またはQ3のいずれか一方はご入力ください。

