授業のワンポイント
体積
■小学校での柱体の体積の学習
直方体を四角柱とみなし,
四角柱の体積=(縦×横)×高さ=底面積×高さ
として求め,三角柱の体積は,四角柱の体積の半分と考え,底面の三角形の面積が四角柱の底面の長方形の半分であることから,「底面積×高さ」として求められることを確認しています。
また,次の図のように,正多角形の底面の辺の数を増やしていくと,ついには円柱になるという考えから,すべての角柱,円柱の体積が「底面積×高さ」で求められることを学んでいます。
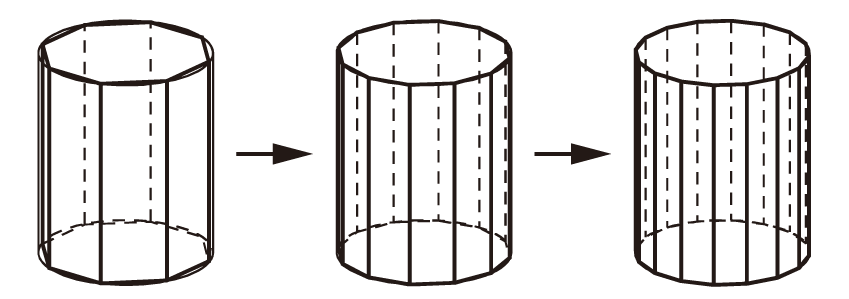
柱体が「面を平行に動かしてできる立体」と考えられることと結びつけて指導することによって,高等学校で積分を用いて立体の体積を求める場合の考え方につながります。
■角錐の体積は角柱の1/3であること
角錐や円錐の体積の求め方の説明には積分が必要であることから,中学1年の段階では,操作的,実証的な方法で説明しています。
ここでは,立体模型を使って説明する方法を2つ紹介します。
1.下の図1の展開図を3つ用意し,底面が正方形の斜角錐を3個組み立てます。この3個の斜角錐をうまく組み合わせると1つの立方体ができあがります。この立方体は,斜角錐と底面積と高さが等しくなります。
このことから,角錐の体積は,底面積と高さの等しい角柱の体積の1/3であることが説明できます。
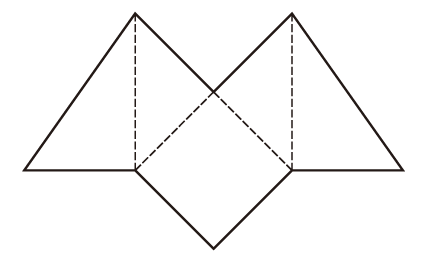
図1
2.下の図2の展開図を6つ用意し,6個の正四角錐を組み立てます。組み立てられた四角錐は,底面が正方形で,高さが底面の正方形の1辺の長さの半分になっています。この四角錐の頂点ができ上がりの立方体の中心になるように組み合わせると,1つの立方体になります。
このことから,錐体の体積が,底面積と高さの等しい角柱の1/3であることが説明できます。
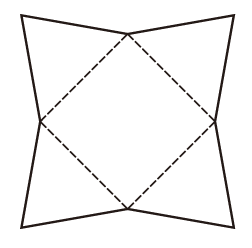
図2
[6章]空間図形
2節 立体の体積と表面積(教科書p.200〜213)
アンケート
よろしければ記事についてのご意見をお聞かせください。
Q1またはQ3のいずれか一方はご入力ください。

