授業のワンポイント

多項式どうしの乗法

■多項式どうしの乗法

　多項式どうしの乗法は，この章の重要な指導内容の1つで，あらゆる式や公式の利用に際しても基礎・基本となるものです。面積図とも関連させて，分配法則を繰り返し適用すればよいことをていねいに指導し，その上で，式の展開の意味を十分に理解させておく必要があります。
　教科書p.14では，(a＋b)(c＋d)＝ac＋ad＋bc＋bd　について，面積図を使って説明することができるだけでなく，分配法則を使って説明することができることを学習します。
　分配法則を使って式を計算するためには，もとの式が多項式と単項式の積の形になっていなければいけませんが，(a＋b)(c＋d)はその形になっていません。これまでに学んだ方法を使って計算するためにはどうすればよいのかを，考えさせることが大切です。その学習の中で，c＋dを1つの文字Mとして考えればよいということを，生徒から引き出します。

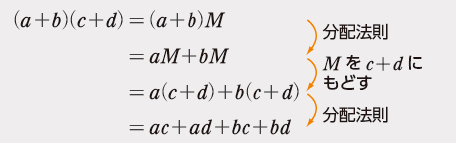
　分配法則を使って計算する中で，a(c＋d)＋b(c＋d)という式が出てきます。c＋d を1つのものとして考えることが，面積図ではどのような意味があるのかについても考えさせてもよいでしょう。

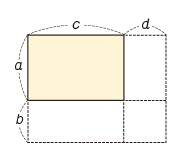
　2つの長方形の面積の合計と考えると，a(c＋d)＋b(c＋d) (m^2)と表すことができる。

［1章］式の展開と因数分解　
1節　式の展開と因数分解（教科書p.10〜27）

記事一覧に戻る

アンケート