授業のワンポイント
平行線
■平行線の定義
ユークリッドの原論では,平行線について,第Ⅰ巻の定義23で,「平行線とは,同一平面上にあって両方向に限りなく延長しても,いずれの方向においても交わらない直線である。」とあります。
また,公準の5において,「1直線が2直線に交わり,同じ側の内角の和を2直角より小さくするならば,この直線は限りなく延長されると2直角より小さい角のある側において交わる」とあります。
しかし,この「同じ平面上にあって交わらない2直線」という定義に従って,平行線を作図することは困難です。
そこで,小学校の教科書では,「1本の直線に垂直な2本の直線は平行である」と平行線を定義しています。あるいは「1本の直線に等しい角で交わる2本の直線は平行である」と扱うこともあります。
つまり,同位角が等しい2直線として平行線が定義されているといえます。
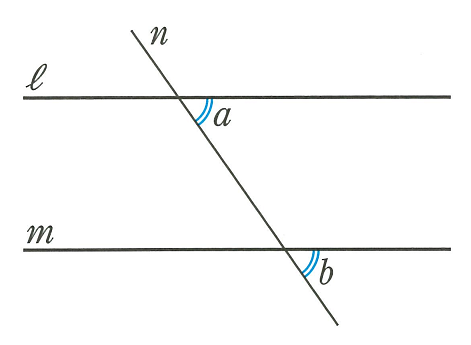
∠a=∠b ならば l//b
■平行線をかく方法
小学校の教科書の定義をもとに平行線をかくには,教科書p.97「ふりかえり」にあるような方法をとることになりますが,このかき方は,1年で学習した定規とコンパスのみを使用した作図とはいえません。
ユークリッドの原論では,第Ⅰ巻命題31において平行線の作図が取り上げられています。それは「錯角が等しい2直線は平行である」という命題27にもとづき,次の手順で行われています。
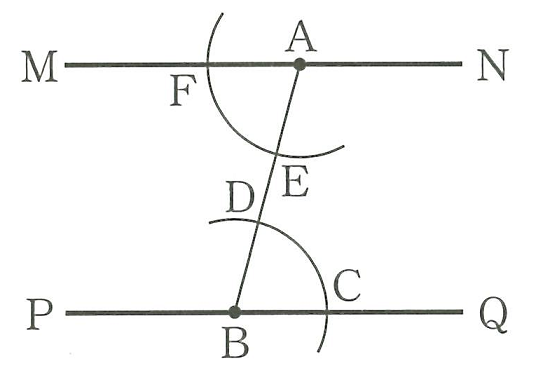
直線PQと点Aが与えられていて,
(1)直線PQ上に任意の点Bをとる。
(2)点Aと点Bを結んで線分ABをひく。
(3)点Bを中心として,適当な半径で円をかく。
(4)点Aを中心として,3の円と同じ大きさの円をかく。
(5)コンパスで線分CDの長さをとり,それと同じ長さの線分EFをとる。
(6)点Aと点Fを結ぶことによって,直線PQに平行な直線MNがひける。
[4章]図形の調べ方
1節 平行と合同(教科書p.94~111)
アンケート
よろしければ記事についてのご意見をお聞かせください。
Q1またはQ3のいずれか一方はご入力ください。

