授業のワンポイント
相似な図形の計量
■相似な図形の相似比と面積の比
この項では,相似な図形において,相似比と面積の比の関係を調べていき,それを定理としてまとめ,その関係が使えるようにすることがねらいです。
この項全体の流れは,
・相似な三角形で証明する
・相似な多角形の例として,五角形で証明する
・相似な多角形に,一般化する
・曲線図形の例として,円で証明する
・一般の相似な図形の性質として,まとめる
のようになります。
とびらで予想した,相似比が1:kのとき,面積の比が1:k^2になることを,まずは,三角形の場合で証明します。
次に,多角形の代表として,五角形でも,三角形の場合と同様の関係があること,また,円についてもいえることを明らかにした上で,一般の相似な平面図形について,相似比と面積の比の関係をまとめていきます。
■相似な立体
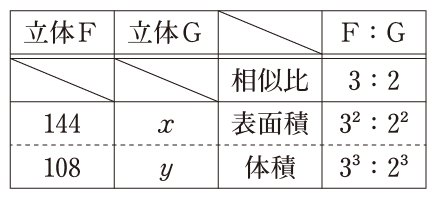
教科書p.151例題1は,相似な立体の表面積や体積を,相似比の関係を使って求める問題です。抽象的な立体F,Gを取り上げているため,どれとどれとの比であるかがわかるよう,くふうして指導する必要があります。
下のように対比させて示しながら,比例式をつくらせるとよいでしょう。
ある立体の表面積や体積がわかっているとき,その立体と相似な立体の表面積や体積は,もとの立体との相似比を知ることによって求められることを実感させましょう。
[5章]図形と相似
3節 相似な図形の計量(教科書p.145〜152)
アンケート
よろしければ記事についてのご意見をお聞かせください。
Q1またはQ3のいずれか一方はご入力ください。

