授業のワンポイント
相対度数
■相対度数の表し方
相対度数は分数で表すこともできますが,用いる目的を考えると小数で表すほうが好都合です。例えば,相対度数が分母の異なる分数で表されていた場合は,2つの階級でどちらの度数が大きいのかを瞬時に判断しにくかったり,その階級の度数の全体に対する割合もわかりにくかったりします。相対度数を求めること自体が目的ではなく,その資料を活用するためにおこなうものなので,活用しやすい形を考えて,相対度数も小数で求めるように指導するのがよいでしょう。
また,四捨五入によって各階級の相対度数を求めた場合に,その合計が1にならない場合もあります。そのときも,全体を1として考えていることを示す意味で,相対度数の合計欄には1.00のように書きます。このとき,合計がちょうど1.00になるように各階級の相対度数を調整する必要はありませんが,円グラフに表したりするなど,特にそれが必要な場合は,相対度数の最も大きい階級で調整することが多いです。
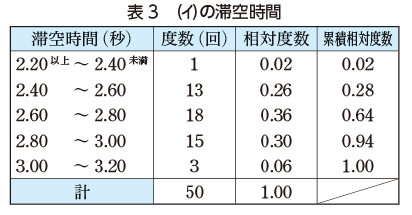
教科書p.225の表
■PPDACサイクル
教科書p.228では,「紙の滞空時間」として,自分なりの課題を設定していて,統計的な問題解決活動の一連の流れをレポートで示しています。このような統計的な課題解決のプロセスは,「PPDAC」ということばで表現されることがあります。
PPDACとは,次の(1)〜(5)の単語の頭文字を並べたもので,(1)→(2)→(3)→(4)→(5)→(1)という流れとサイクルの繰り返しを意味しています。
(1)Problem :課題の発見,設定
(2)Plan :データの収集と分析の計画
(3)Data :データの収集,記録,整理
(4)Analysis :データの分析
(5)Conclusion :結論の取りまとめ
[7章]データの活用
1節 ヒストグラムと相対度数(教科書p.214〜232)
アンケート
よろしければ記事についてのご意見をお聞かせください。
Q1またはQ3のいずれか一方はご入力ください。

