授業力をみがく

地球上の2地点間の距離（大圏航路）

岐阜大学教育学部　教授　河崎 哲嗣


　皆さん、新年度を迎え新たな気持ちで臨んでおられることでしょう。ドイツへ研修に勤しんでおられた先生も、無事に学校現場に復帰されました。
　コロナ前までは、公立学校でも少しずつ海外への研修旅行が増えておりました。西欧までの長旅。10時間近くのフライト時間は、ぐっすり眠れるかといえばそうでもありません。とても退屈な長時間は、前座席後部に設置されているモニターを操作して、日本で未公開の映画やゲームを楽しみ、少しでも気分を癒やそうとします。また、現在どの地点の上空を飛んでいるのか、それまでの経路などを確認することもできます。航空機等の運搬は、燃料エネルギーの節約や移動時間を短縮するために、地球上の2地点を結んで最短コースを利用するのですが、地図上の2点を結んだ直線よりも、少し曲線を描く大圏航路を利用するということを社会科の授業等で学んだことでしょう（偏西風のお陰で、同じコースでも「西から東」へは早く移動できますね）。

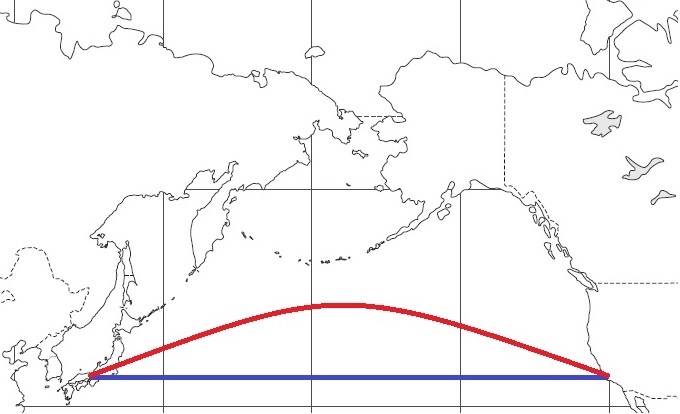
　球の中心を通る平面で切り取る断面図は円（大円）になります。地球を球体と仮定した場合、世界の2都市を結ぶ弧は無数に存在しますが、そのうち最短距離となるのは、弧が大円上の一部分になるときです。具体的に地球儀を前にして、じっくりと眺めて考えてみてください。地球の位置は、緯度と経度で把握し、その線はどのように引かれているのかも確認してみてください。緯線は赤道に平行な線であり、経線は北極・南極を結んだ大圏ラインであることが分かります。何故、緯線と経線の引き方にこのような違いが生まれたのか不思議ではありませんか？
　人類が「時間を把握する」ことの重要性に気づいてから、身の回りの生活に馴染んで使用している機械時計の製作に至るまでに、いろいろな時計を創り出しています。西欧の各旧市街を歩けば、緯度の異なる所にはそれぞれ重要な痕跡（時計）が分かるのですが、この話は別の機会にいたしましょう。


　ところで、小学校5年生の社会科の教科書では、緯度・経度を学んだ後で、地球儀上の2点間を紐で結んでその長さを測り、地球儀と実際の地球の半径の長さの比から、地球上の2地点間の最短距離を算出しています。また、インターネット上で2地点の緯度・経度を入力すれば、自動的に求められるようにもなっています。しかし、これが具体的にどのようにして求められているのかの基本を考えたことはあるでしょうか？　便利過ぎた社会に慣れてしまい、その背景の数学や科学を見失っていないでしょうか？
　私がまだ教諭だった頃、高校1年生の学年研修旅行先がシンガポールでした。その事前学習に、「学校からマーライオンまでの距離を求めなさい」というのを冬休みの課題として与えました。具体物を使って緯度・経度の確認をしてから、高校1年生での既習内容に当たる「三角比の定理」の利用を勧めて、地球上の2地点間の距離を算出する内容です。

　当時の担任した自然科学系クラスは、「大学受験に関係ない」「教科書に書いていない」などと否定的に捉えている生徒達が多く、冬休み中に取り組んだ者はクラスの半分程度で、そのときは相当落ち込んだものでした。ところがその1ヶ月程度後、その年度の京都大学の入試に緯度・経度を利用した2地点間の距離に関する問題が出題されたのです。朝のSHRで話しながら、その記事を後ろの黒板に貼りだしたのを憶えています。そして、ドイツの高校数学の教科書の内容を例に、頻繁に扱われている教材を示して、生徒達のグローバルに対する視野の狭さや閉鎖的なものの考え方をたしなめたものです。


　冒頭でお話した2年間のドイツ研修から帰国される先生に、「経路の写真を撮っておいて！」と頼みました。よく知っている大圏航路に近い平常のコースは、絶対に使用していないという確信があったためです。現状の把握を理解するとても良い題材になると考えたのでした。

--------------------------------------

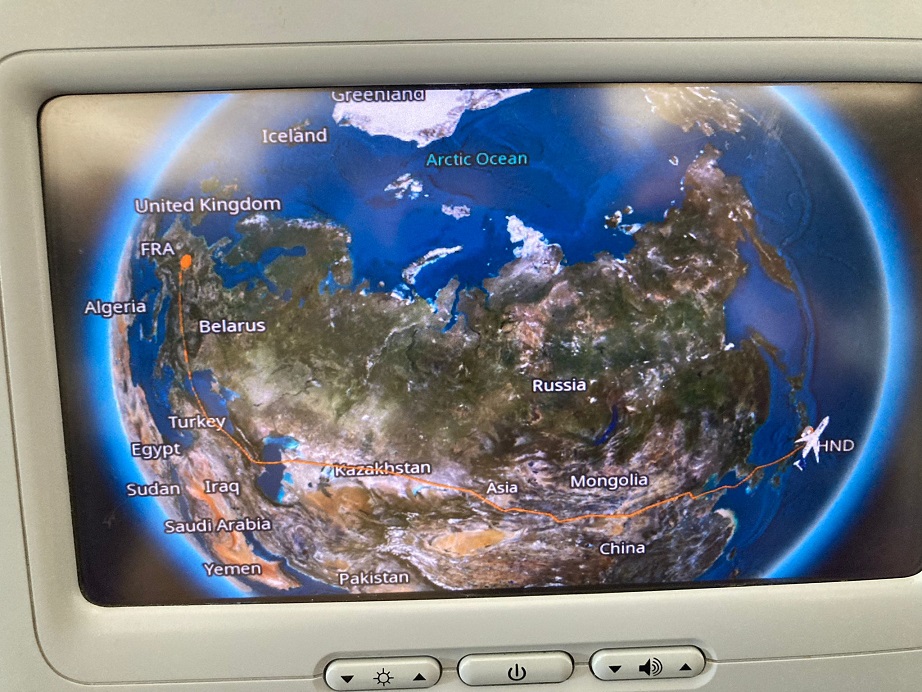
河崎哲嗣（かわさき　てつし）　　
1964年生まれ
数学科教諭として、23年間京都府立高等学校・京都教育大学附属高等学校に勤務
2002年　京都教育大学大学院教育学研究科（修士課程）修了
2016年　大阪大学人間科学研究科博士後期課程修了　
2016年　博士（人間科学）大阪大学
現　職　東海国立大学機構 岐阜大学教育学部教授
専　 攻　数学教育学，教育工学，国際遠隔協働学習，STEAM

記事一覧に戻る

アンケート