授業のワンポイント
確率の求め方
■確率の求め方
この章の指導においては,「同様に確からしい」ということを根拠にして,簡単な場合についての確率を求めることができるようにします。そして,確率を用いて,不確定な事象を捉え考察し表現できるようにします。1年で学んだ統計的確率と関連づけながら,理解を深めていきましょう。
教科書p.166では,1つのさいころを投げる事象を扱い,これまでの実験によって求めてきた統計的確率(経験的確率)から,実験によらないで求める数学的確率(先験的確率)を考えます。その際,統計的確率から数学的確率へと数学的な見方をひろげていることを実感できるようにすることが大切です。
実験によって得られた1の目が出る確率1/6が,すべての目の出る場合の数(6通り)に対する,1の目が出る場合の数(1通り)の割合1/6にほぼ等しいと考えられることに注目させましょう。
また,確率の求め方を,枠囲みにまとめてありますが,特に,場合の数を考えるとき,どの起こり方も「同様に確からしい」という前提で確率を求めていることを強調する必要があります。いろいろな確率を求める際に,この枠囲みの内容を常に確認することが大切です。
■確率の意味をふり返る
教科書p.168の「数学的活動」では,場合の数をもとにして求めた確率の意味について話しあい,確認する活動です。
確率については,1年において,「あることがらの起こりやすさの程度を表す数」として定義していますが,生徒は場合の数をもとに確率を求める学習を進めていく中で,その意味を忘れがちです。
特に,ことがらが不確定であることの理解が十分できていないために,「あることがらがかならず起こる」と考える生徒は少なくありません。かりんさんの「実験を9回おこなえば,赤玉が,かならず9回出る」という考えも,けいたさんの「実験を900回おこなえば,赤玉が,かならず400回出る」という考えも,正しくないことに気づかせるようにしましょう。
かりんさんとけいたさんの確率についての考えの正誤について話しあい,確率の定義にもとづいて判断する活動を通して,不確定な事象に関する確率の意味をふり返って確かめることが大切です。
■いろいろな確率
「確率の求め方」の項で学習した確率の求め方をもとにして,いろいろなことがらの場合の数を考え,確率を求めることができるようにします。樹形図や表などを用いて,もれや重なりがないように場合の数を求めることができるようにし,これらを用いて,硬貨やさいころなどを投げたときの確率を求めることができるようにしましょう。
確率を求める際に必要な場合の数を求めることについては,小学校6年でも学習しています。しかし,樹形図や表などを用いて表現することに十分習熟しているとはかならずしもいえません。
教科書p.169では,もれや重なりがないように場合の数を求めるための方法について理解させ,積極的に活用できるようにしましょう。
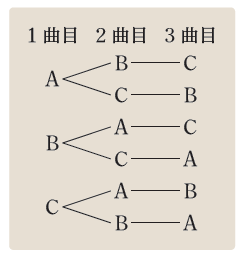
樹形図
[6章]場合の数と確率
1節 場合の数と確率
(教科書p.164〜175)
アンケート
よろしければ記事についてのご意見をお聞かせください。
Q1またはQ3のいずれか一方はご入力ください。

