今知りたい授業のワンポイント

角柱の体積

■角柱の体積公式

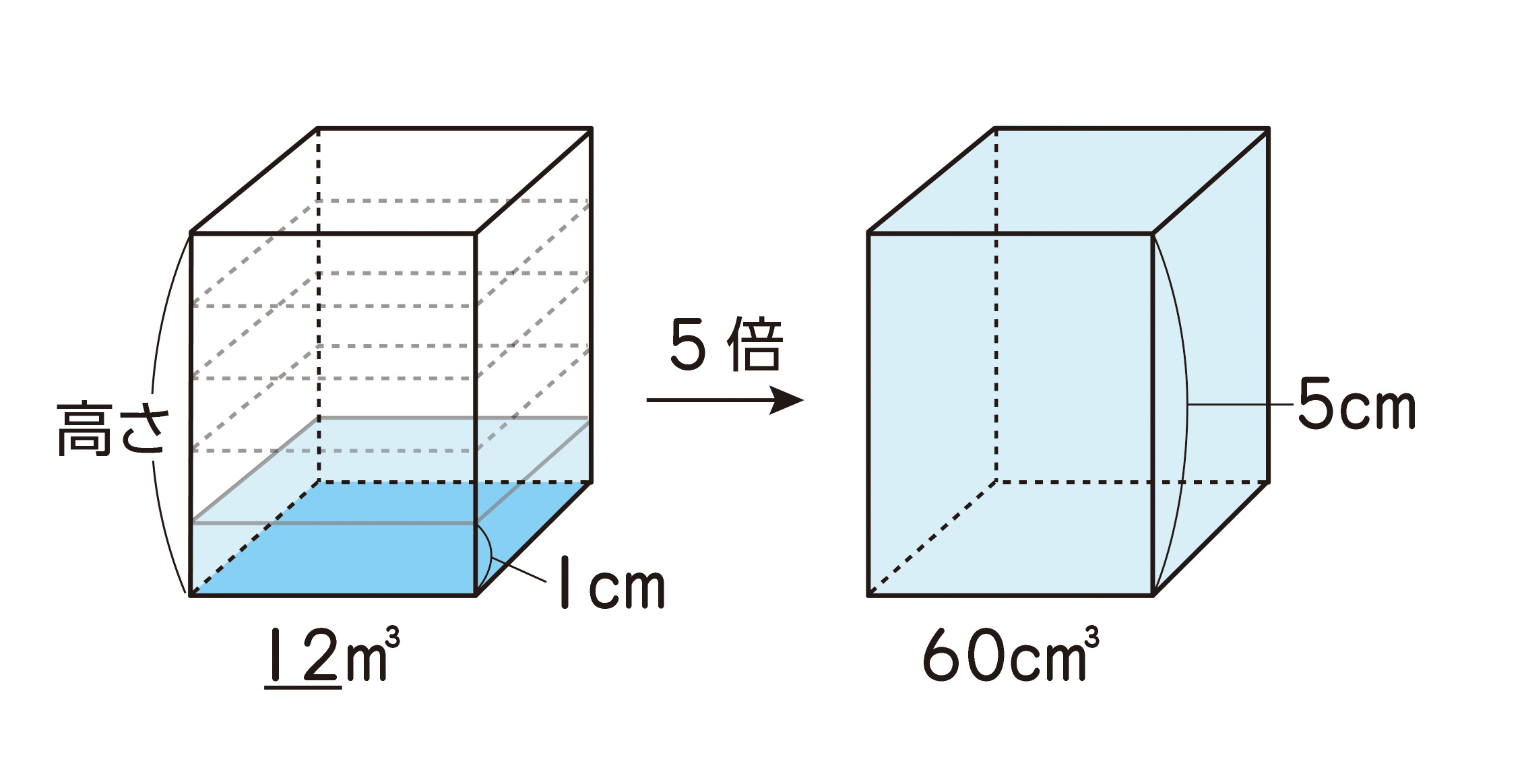
　児童は、第5学年で直方体の体積について学習したのち、縦と横の長さを変えずに高さだけを2倍、3倍、……にすると、体積も2倍、3倍、……になるという比例関係を学んでいます。
　そのときの学習を想起することで、高さを1（cm）とした場合に着目させ、「直方体の体積＝｛高さ1（cm）の角柱の体積｝×｛積み上げた段数（高さ）｝に気づかせるようにしましょう。
　また、「直方体の体積＝縦×横×高さ」の式の右辺を結合法則によって「（縦×横）×高さ」とくくると、括弧内の縦×横が底面に並んでいる単位立方体の数であり、これが底面積の値と等しくなることを理解させましょう。

■角柱の体積の求め方を「底面積×高さ」でまとめる

　一般の四角柱の体積は、三角柱に分割すると求められますが、

　教科書p.101 [お]の体積＝（8×3÷2）×5＋（8×4÷2）×5
　＝（8×3÷2＋8×4÷2）×5

というように、式を変形することによって、やはり「底面積×高さ」で求められることがわかります。さらに、どんな角柱でも三角柱に分割できることから、「角柱の体積＝底面積×高さ」で求められるというようにまとめていきましょう。
　上述のような式変形は戸惑いを感じる児童がいると思われます。そのため、三角柱に分割して求めたときの結果と、「底面積×高さ」で求めたときの結果を比較し、同じ結果が得られることを確認させるようにしましょう。

［8］立体の体積（教科書p.98〜105）

記事一覧に戻る

アンケート