今知りたい授業のワンポイント

見積もりの素地

■数の見方を働かせて判断する

　第1学年では、48円のチョコレートが50円で買えるかどうかを判断する学習をしています。そこでは、48と50という数の大小を比較して判断しました。第2学年の「買えますか？　買えませんか？」では、1つが100円で買えるか買えないかの判断をもとに、いくつかの品物が何百円で買えるか買えないかを判断し説明することができるようになるのがねらいです。

【100をこえる範囲での見積もり】
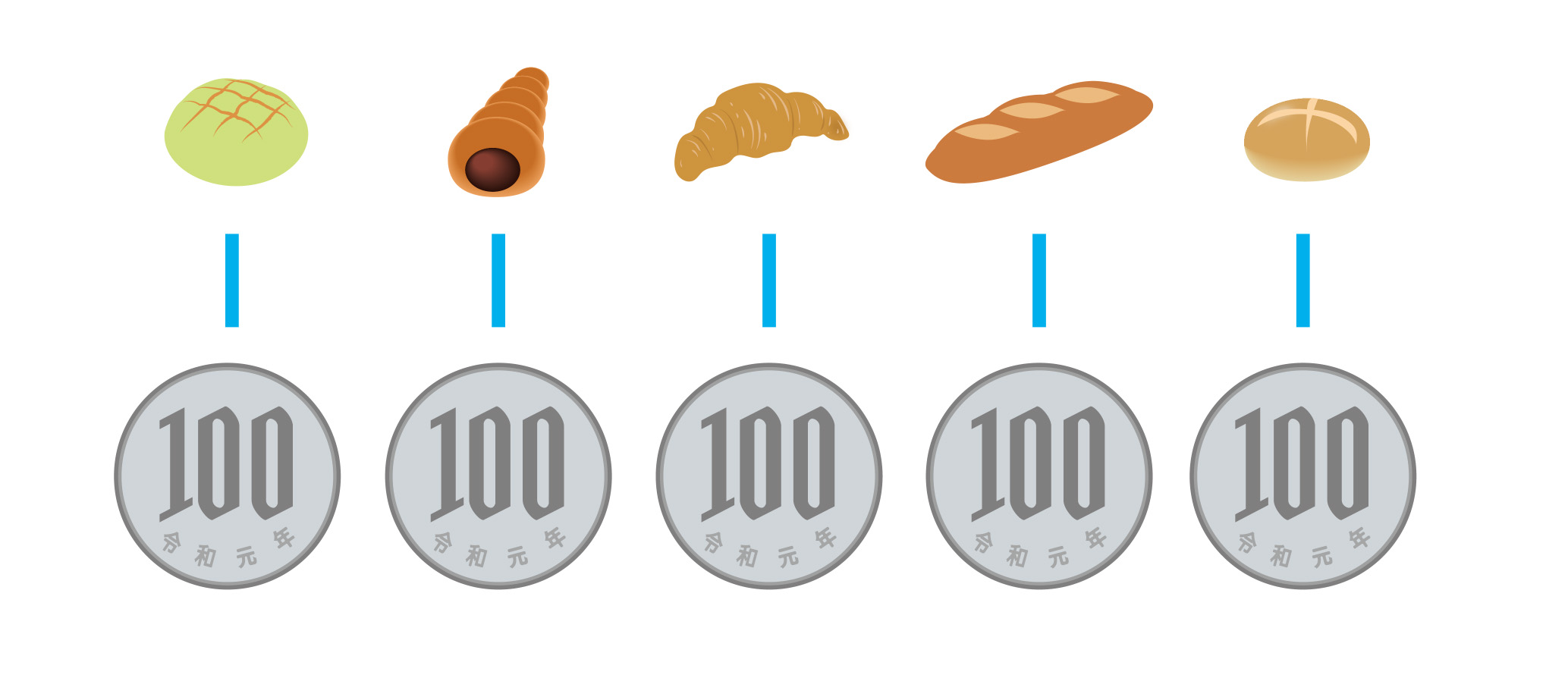
　p.96の［1］で取り上げている問題は、100をこえない範囲での見積もりです。「500−（98＋98＋98＋98＋98）＝10で、おつりが10円なので買える」と判断するのではなく、「500円を百円玉5枚とみて、100円で98円のパンを1つ買える」と判断させます。

【100をこえない範囲での見積もり】
　p.97の［2］で取り上げている問題は、100をこえる範囲での見積もりです。ここでも、「300−（105＋105＋105）でひけないので買えない」と判断するのではなく、「105は100より大きいことに着目して、100円をこえるので買えない」と判断させます。

　100が何個という数の見方をすることで、計算しなくても簡単に判断することができます。その見方と、その見方を働かせるよさを感得させるようにしましょう。そのためにも、［1］では、500円のお金の図は500円玉1枚ではなく、100円玉5枚とみて、パンと100円玉の図を見て考えるように促しましょう。
　なお、1つが100円で買えるかどうかがわかっても、それをいくつも組み合わせるとつまずく児童もいます。2つが200円で買えるかどうか、3つではどうか、というように順を追って指導するとよいでしょう。

■見積もりの根拠を明らかにする

　1つが100円で買えるかどうかで判断することが大切ですが、その説明の際に、「品物の絵とお金の模型を使ってみると」や「図にして考えてみた」など、自分が判断できた根拠をわかりやすく伝えようという意識をもたせ、対話的な学びとすることも大切です。

買えますか？　買えませんか？（教科書上巻p.96〜97）

記事一覧に戻る

アンケート