今知りたい授業のワンポイント

分数

■もとの大きさの半分の大きさであることを確かめさせる

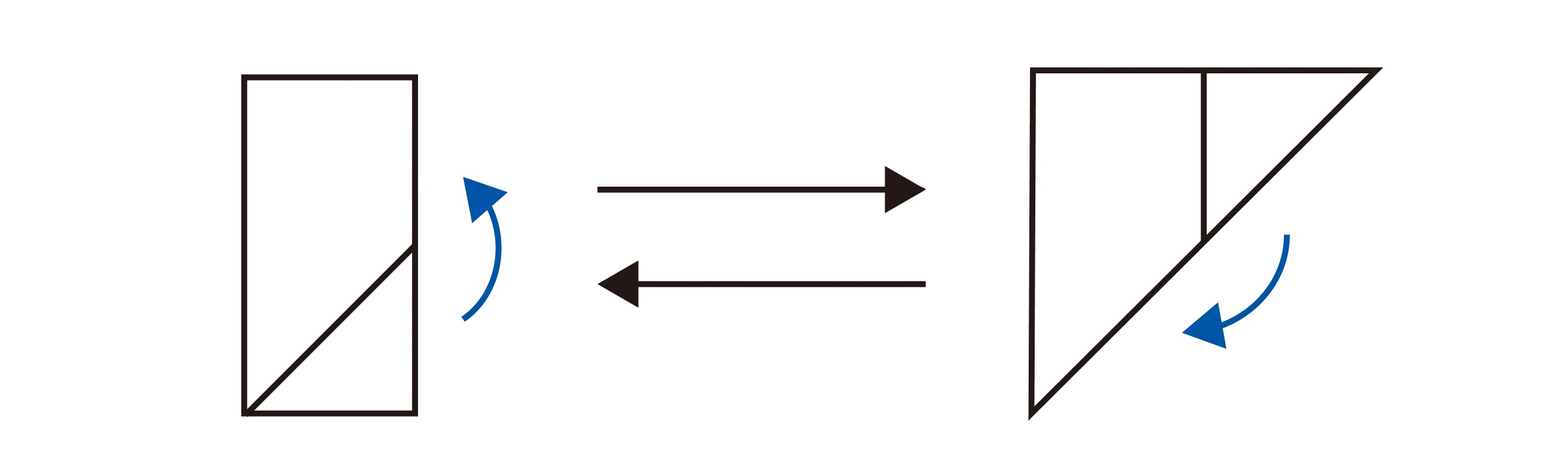
　教科書p.104で半分の形を発表させるときには、本当にもとの大きさを同じ大きさに2つに分けているといえるかを確認させましょう。それによって、形が違う場合もすべてもとの大きさの半分になっていることを捉えさせることができます。ただし、ぴったり重なるものは同じ大きさであることがわかっても、形が違うときに同じ大きさかどうかを判断することは難しいことです。そういった場合には、等積変形によって同じ大きさかどうかを捉えさせてもよいでしょう。例えば、正方形の半分である長方形と三角形を比べる場合、下のようにつくり変えることができます。

■割合の素地・除法の素地

　教科書p.108〜109では、分割分数の意味に基づいてはいますが、●の図を使って1/2や1/3の大きさを表す活動と考察を通して、割合の素地的活動を行っています。
　まず、12個の●の図を使って、12個の1/2は6個、逆に、6個の2倍は12個という捉え方ができることに触れます。これは、割合でいうところの基準量と比較量を入れ替えたときの見方に相当するものです。このことを踏まえて、●が18個の場合について考えさせて、18個の1/2は9個、逆に9個の2倍は18個ということを、図を使って説明させます。さらに、●が12個や18個の場合で1/3の大きさを考えさせることを通して、同じ1/3であっても、もとの●の数が違うとその大きさは違ってくることに気づかせます。これは、割合が同じでも基準量が違えば比較量としては違ってくるということを扱っています。

　以上が割合の素地的活動としての解説ですが、わり算が未習であることを踏まえると、わり算の素地的指導という解釈もできます。そして、わり算の素地としてみると、分数の表記を用いてはいますが、乗除の関係を扱っているということもできます。
　いずれにせよ、p.103〜107で学習した分割分数の文脈から、もとにする大きさとの関係をさらに強調することで、割合の見方（乗除の関係）にまで踏み込むことになります。抽象的な議論では大変理解しにくい内容であるため、必ず、●の図を使って考えさせたり、話しあわせたりしましょう。

17.分数（教科書下巻p.103〜109）

記事一覧に戻る

アンケート