今知りたい授業のワンポイント

何倍になるかを考えて

■2通りの考え方で解く

　教科書p.134[1]は、次の2通りの考え方ができます。

ア．順に考えていく方法
　　まず、百貨店の高さを求める。90÷3＝30
　　次に、学校の高さを求める。30÷2＝15

イ．まとめて何倍になるかを考える方法
　　テレビ塔は学校の高さの何倍かを求める。2×3＝6
　　学校の高さを求める。90÷6＝15

　アは、これまでの考え方で解決したもので、ほとんどの児童が考えつく解法です。イは、「何倍になるかを考えて」という思考法を用いた解法です。このような2通りの考え方について、教科書の図をもとに児童に説明させるとよいでしょう。そして、どちらの方法も認めながら、イのオペレータ（変量）による計算に着目させ、新しい考え方のよさに気づかせるようにしましょう。

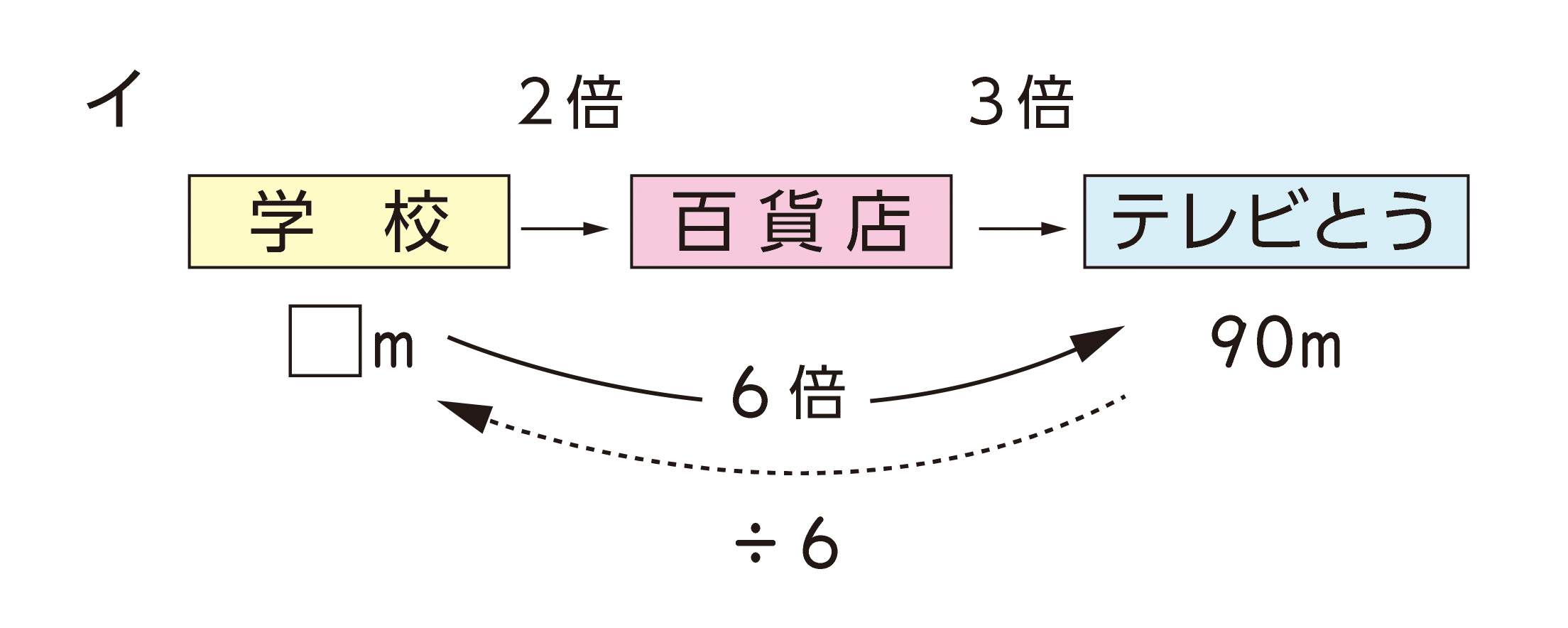
■関係図を活用して、数量間の関係を捉える

　関係図は、それぞれが何倍になるかを略図的に表したものです。このような図に表すと、何が何の何倍なのか、また求めるのはどこかなどが大変明確になります。
　関係図の見方については、第3学年の「何倍でしょう」で扱っているので児童も理解していると思われますが、再度確認させましょう。
　そして、何倍になるかを考えて解いた式について、例えば、3×2＝6の「3×2」は関係図のどこを表しているのか、72÷6＝12の「72÷6」は関係図のどこから導かれているのかなどを話し合いの中で明らかにさせ、図と式を対応させるように指導しましょう。

9.割合（教科書上巻p.128〜135）

記事一覧に戻る

アンケート