今知りたい授業のワンポイント

九九の表とかけ算

■a×0、0×aの指導

　0のかけ算の意味を理解することは、第3学年にとって簡単なことではありません。0をかけた積が0であるということは、数学的にそうした整合性があるという「約束事」の側面があるからです。そこで教科書p.13では、「おはじき入れ」という具体的な場面を取り上げて、積が0となることを児童に自然に受け入れさせるようにしています。
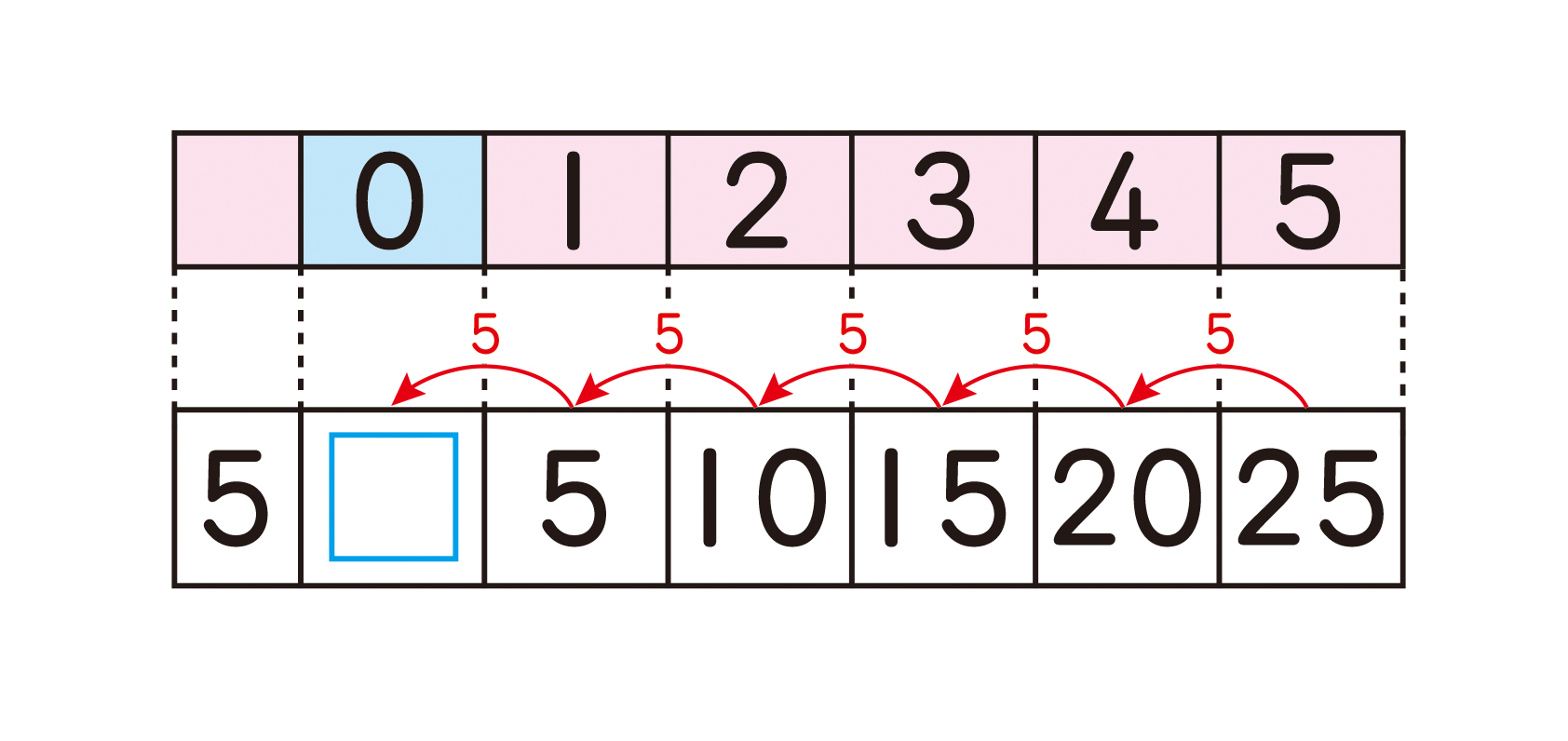
　（点数）×（入った個数）＝（得点）であることから、5×0については「1つも入らなかった」と捉え、5点の得点についても5×0と立式できるのはないかと考えさせましょう。5×0の積については、下の図のように、5の段の九九の積の変化に着目すると、5×1より5小さくなることから、5×0＝0となることを導きます。さらに、再度具体的な場面に即して「5点のところには1つも入らなかったので、0点である」という意味づけをして、結果について具体的な納得をさせておくことも重要です。
　5×0については、「入るべき5点の箇所におはじきが入らなかった」ということから0点と考えさせてもよいでしょう。また、0×2については、「0点のところに何個入っても得点は0点である」と考えさせてもよいですし、2×0をもとに交換法則を利用して0×2＝0となることを導いてもよいでしょう

■昔の九九の表

　教科書p.17の「昔の九九の表」は江戸時代の和算の本である『古今算法記』に挙げられている九九の表です。
　このような九九の表は「半九九（はんくく）」と言われています。乗数と被乗数を入れ替えて得られるものは、乗法の交換法則を前提として表から省かれています。したがって、九の段では「九九　八十一」のみが、八の段では「八八　六十四」と「八九　七十二」のみが載っています。

1.九九の表とかけ算（教科書上巻p.10〜17）

記事一覧に戻る

アンケート