今知りたい授業のワンポイント

小数の大きさ

■数としての小数

　児童は既に、分数の学習において、量を表す分数から数としての分数へと抽象化を行っています。そこで、小数の抽象化も、分数の場合と同様に考えさせるようにします。
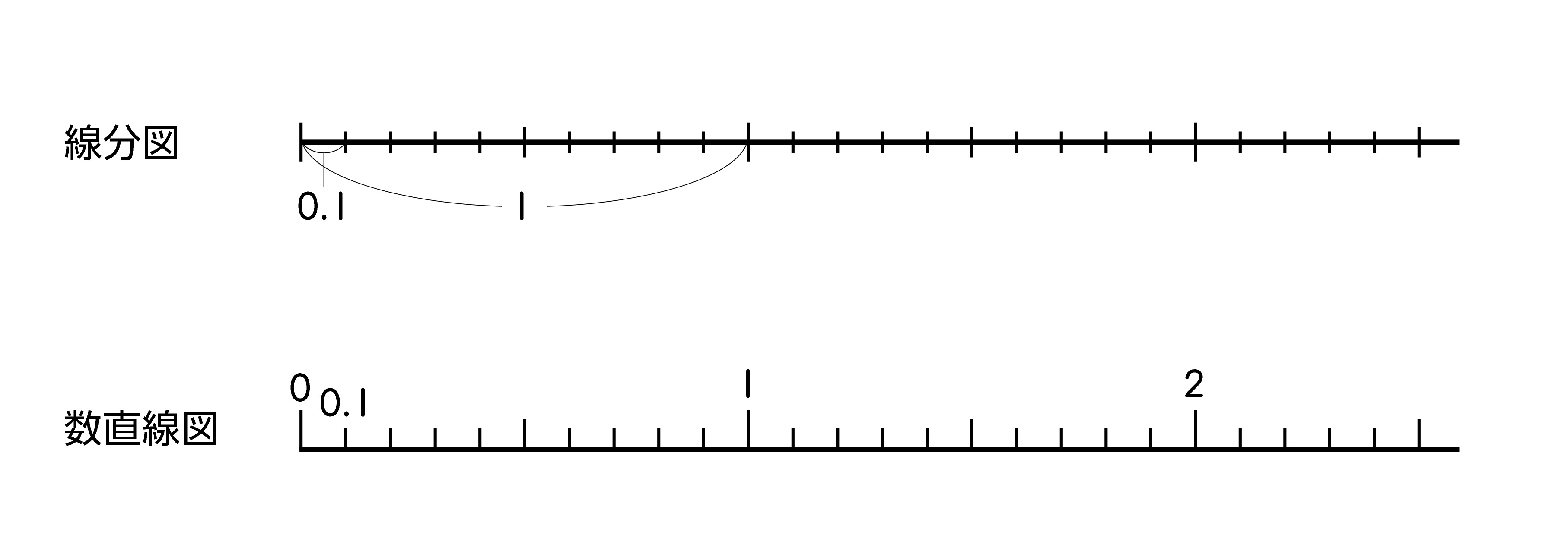
　指導にあたっては、まず、線分図を使って、0.1は1を10等分した1個分の数であり、0.1を10個あわせた数が1であることを理解させましょう。そしてこの後で、次の2つの見方から2.3はどんな数かを考えさせるようにします。

＜数の構成的な見方＞
　2.3は1を2個と0.1を3個あわせた数

＜数の相対的な見方＞
　2.3は0.1を23個集めた数

■数直線の活用

　数直線は直線上の点に数を対応させたもので、実際には第1学年から取り扱ってきています。それは次のようなよさがあるからです。

　1．数直線は、数の幾何学的な表現の1つであり、数の位置（系列）、大小（順序）関係、演算の意味などを見ていくのに役立ちます。
　2．量の大きさと数の大きさを円滑に結びつけ、数を抽象化していくのに役立ちます。
　3．新しく導入した数を、既知の数と関連させて、数として仲間入りさせていくのに役立ちます。

　なお、数直線は数を直線上の点の位置で表すのに対し、線分図は数量を線分の長さで表すところに特徴があります。児童に図を使って説明させる場合にも、数直線図と線分図を区別させましょう。

18.小数（教科書下巻p.68〜81）

記事一覧に戻る

アンケート