今知りたい授業のワンポイント

円柱の体積、体積の求め方のくふう

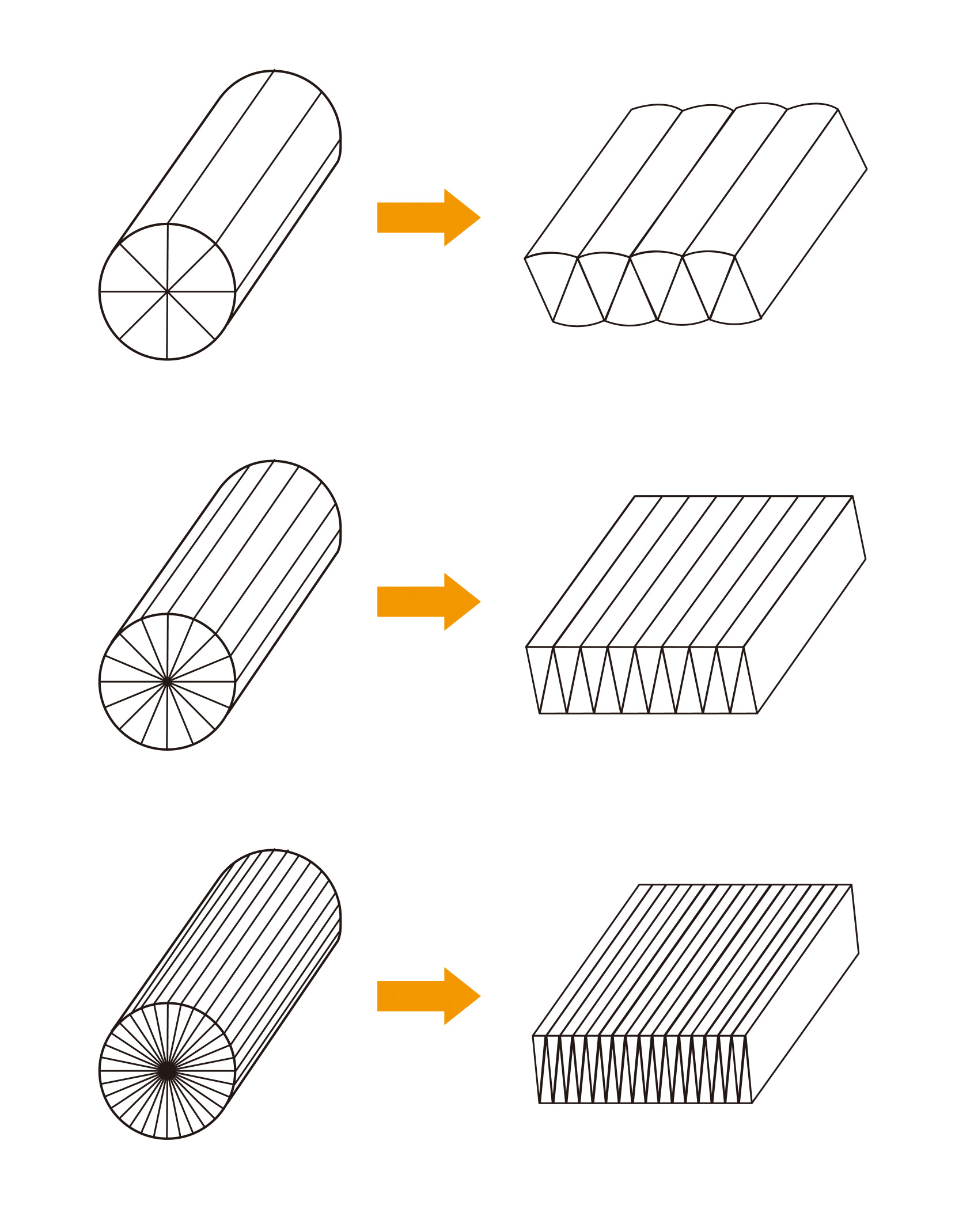
■角柱の辺の数を増やしていくと円柱になると考える

　教科書p.102では、円柱の体積も角柱の体積と同じように「底面積×高さ」で求められることの根拠として、角柱の辺の数を増やしていくと、円柱になるという考え方を取り上げています。これは、底面が多角形の角柱からの類推です。
　なお、「7　円の面積」では、円を分割して長方形に帰着させていることから、下のように円柱を分割して直方体に等積変形しようとする児童がいれば、その考え方を取り上げてもよいでしょう。

■立体図形のとらえ方

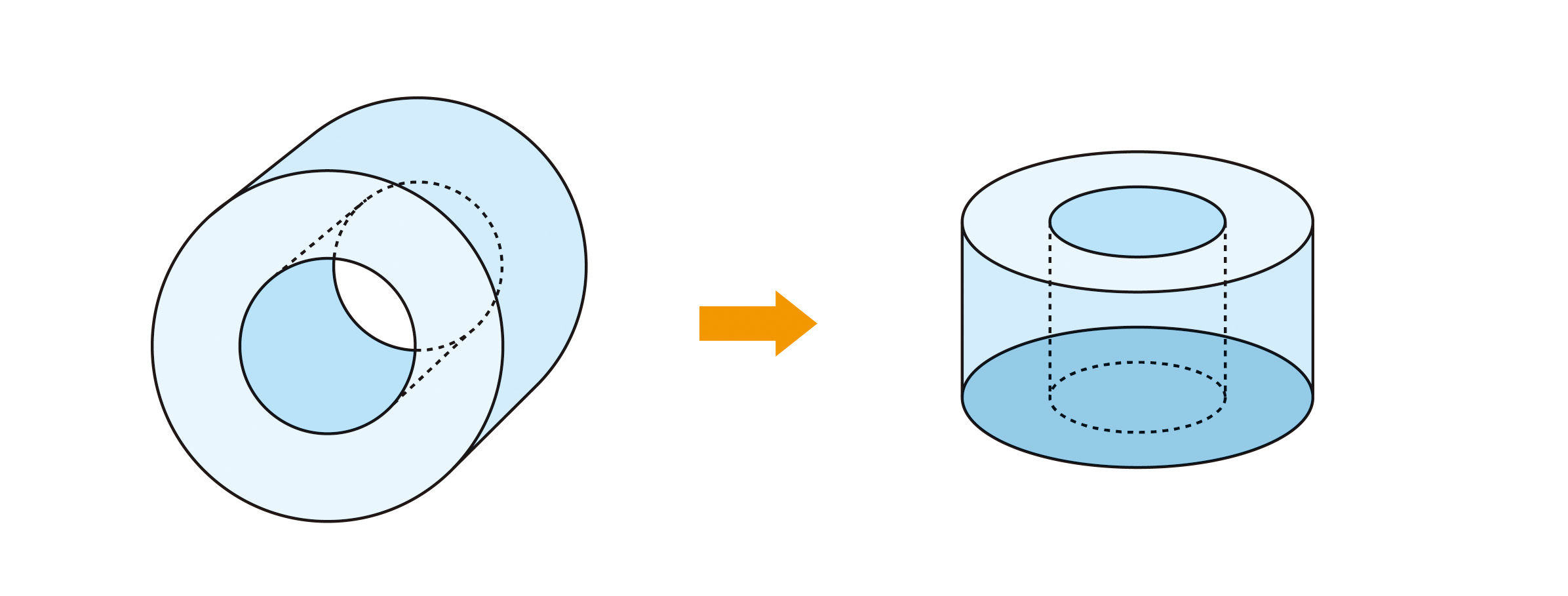
　柱体はその置き方によって柱体に見えないことがあります。立体図形が柱体に見えれば、底面に着目することはたやすいでしょう。図形を一方向からだけでなく多方向から捉えることが重要です。
　見取り図だけを見て念頭で考えることが困難な児童には，具体物を観察させたり、教科書p.109の（し）であれば、トイレットペーパーというように身近なものでその形の特徴を捉えさせたりするとよいでしょう。

8.立体の体積（教科書p.98〜105）

記事一覧に戻る

アンケート