今知りたい授業のワンポイント

比例

■対応する数値に着目させる

　伴って変わる2つの量があるとき、一方の量が増えると他方の量も増えるというような表面的な見方しかできない児童がいます。また、数値に単位をつけて、時間の2倍が数量になるわけがないなどと考える児童もいます。対応する数値に着目することを十分に理解させる必要があります。
　児童の発言をもとに、［時間］×2＝［水の深さ］や［水の深さ］÷［時間］＝2というようなことばの式をつくり、それにあてはめさせて確認していくとよいでしょう。

■比例の定義と性質

　比例を定義する場合、次の2通りがあります。
　1．伴って変わる2つの数量があって、一方が2倍、3倍、…になると、他方も2倍、3倍、…になる。
　2．伴って変わる2つの数量があって、対応する値の商が常に一定である。

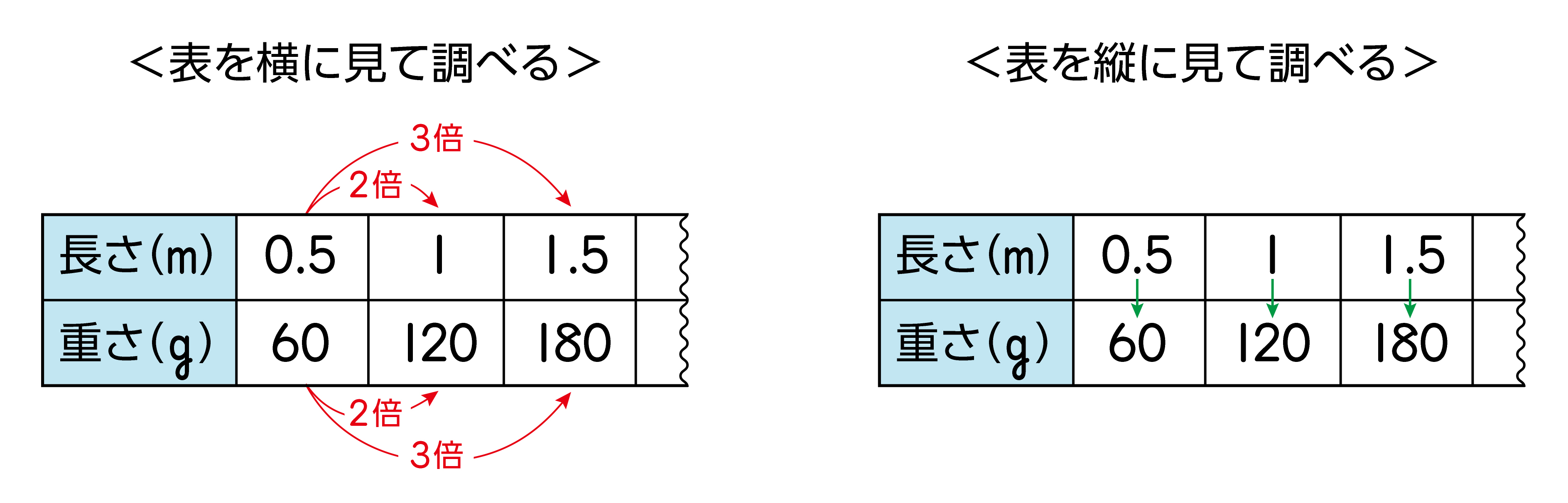
　この2つの表現の仕方は、xとyの値の対応表でいえば、1は表を横に見ていくことであり、2は表を縦に見ていくことです。また、1は比例する事象の判断に役立ち、2は比例の式にすぐに結びつくなどの特徴があります。1、2は内容としては同値であって、どちらを定義としてもよいですが、教科書では、学習指導要領に示されているように、児童の発達段階を踏まえ、1を比例の定義、2を比例の性質としています。
　ただし、中学校では2が比例の定義となります。そのことを意識し、教科書p.156では、1と2の両方で比例を説明するようにしています。

12.比例と反比例（教科書p.154〜181）

記事一覧に戻る

アンケート