今知りたい授業のワンポイント

10倍した数、10でわった数

■10倍した数の一般化

　教科書p.65では、20円の10倍が200円であることから、「20×10＝200」と式に表し、「10倍すると位が1つ上がり、右はしに0を1こつけた数になる」と一般化しています。
　その際、教科書で取り上げている「20円の10倍」と「25円の10倍」という2つの例だけで一般化することなく、「30円の10倍」、「40円の10倍」、……と、「35円の10倍」、「45円の10倍」、……についても同じ考えで答えを求めることができるという経験をさせておきましょう。

■10でわった数の一般化

　教科書p.68では、10個で50円のあめ1個の値段を求める場面を例にとって、50を5×10と考え、50÷10＝5であることを理解できるようにしています。
　そして、さらに250を25×10と考えて、250を10でわった数を25であると求め、それを「250÷10＝25」と式に表し、「10でわると位が1つ下がり、一の位の0をとった数になる」と一般化していきます。

　10でわった数についてまとめる際には、10倍した数についてのまとめと比較するようにします。
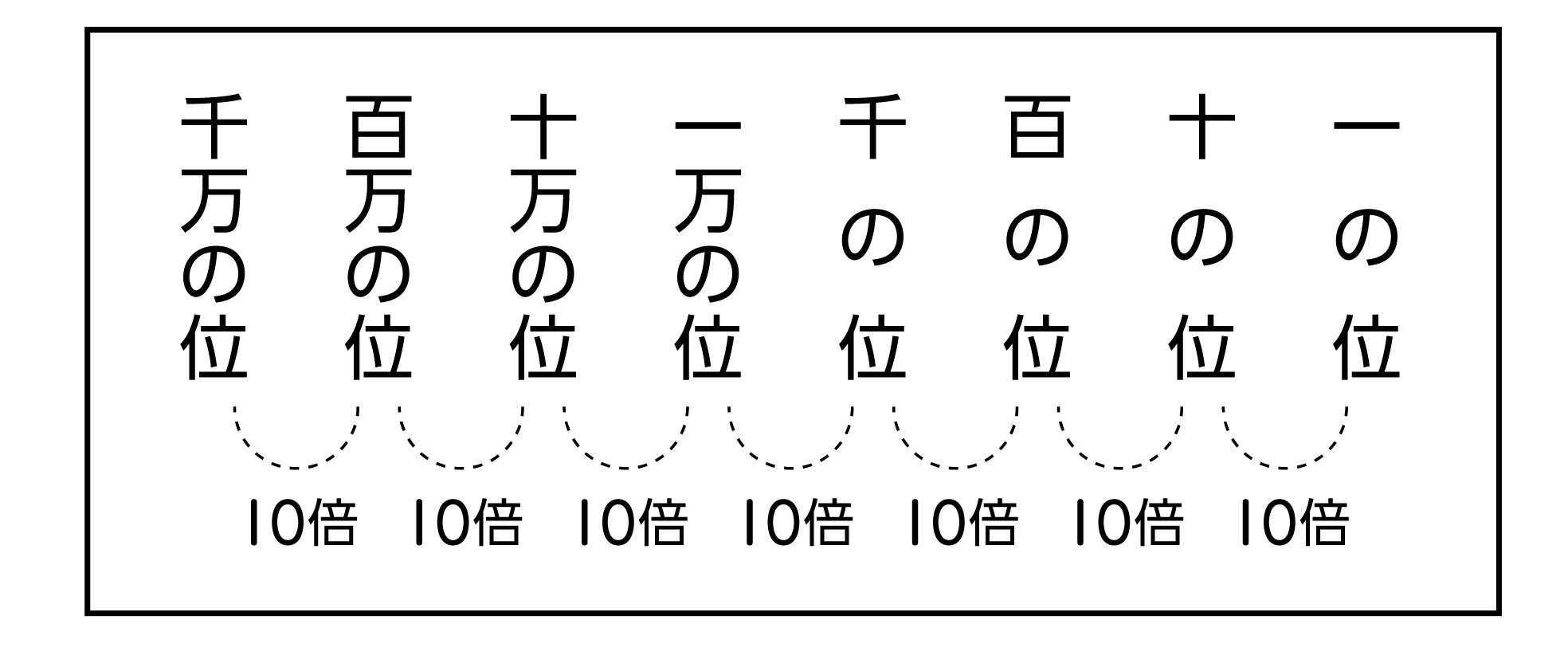
　10倍する（10でわる）ことによって、位が1つ上がる（下がる）ということは、各位の数字の並びが同じまま、左（右）へ位を1つ移動するということです。
　このことは、十進位取り記数法と深く関わっています。十進位取り記数法は、10倍ごとに単位を決めるという仕組みによって成り立っています。
　十進位取り記数法についてまとめるのは、第4学年において億の位や兆の位について学習したあとです。ここでは、その素地となるように、十進位取り記数法の仕組みについての関心を深めておくことが大切です。

［5］一万をこえる数（教科書上巻p.56〜71）

記事一覧に戻る

アンケート