今知りたい授業のワンポイント

分数をかける意味と立式

■分数をかける意味と立式

　分数をかけるということは、整数をかけるときのように同数累加では説明がつきません。そこで、小数のかけ算と同じように、具体的な場面を通して比例関係を見出して、ペンキの量が分数になってもかけ算の式でよいことを説明させていきます。

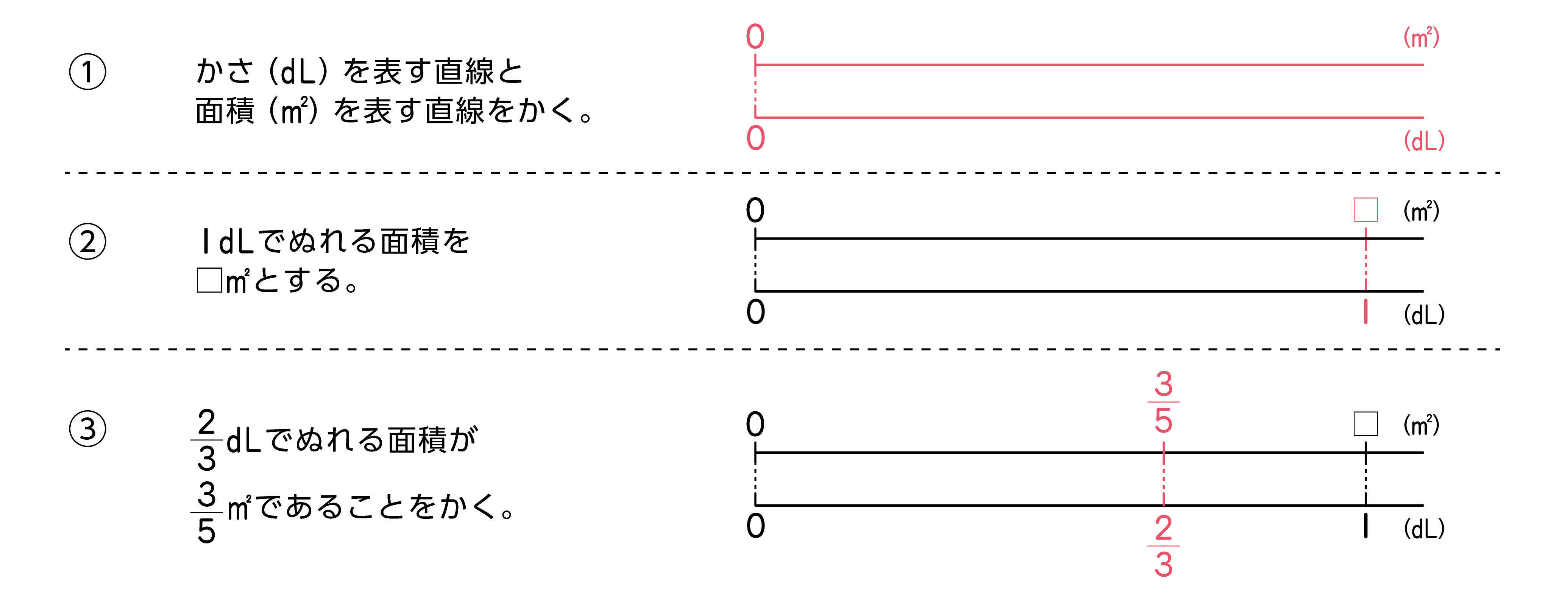
　説明においては、1dLで塗れる面積4/5m^2と、1/3dLで塗れる面積□m^2の関係を表す直線図や関係図を用いるとよいでしょう。数直線図では、1/3dLで塗れる面積が1dLで塗れる面積4/5m^2より小さいことを確認しておくと、計算結果の見通しをもつことができます。また、教科書のp.45以降の立式においても図を活用できるように、p.264にそのかき方が示してあります。

　数直線図や関係図は、複雑な場面でも図を使って数量の関係が把握でき、解決する方法（演算）がわかります。数が小数や分数になると、数の大小関係だけで演算を決めることはできません。そこで、数直線図を使って数量の関係を把握することが有効になります。
　教科書p.265の問の場合、ぬれる面積がペンキの量に比例することをもとにして、ペンキの量が2/3倍になるとぬれる面積も2/3倍になると考えて立式します。

【問】
2/3dLで3/5m^2ぬれるペンキがあります。
このペンキ1dLでぬれる面積は何m^2ですか。

＜数直線図のかき方＞

■分数のかけ算の立式の際は、ことばの式にあてはめる

　整数倍だと何倍かを捉えやすいですが、かける数が小数や分数になると何倍かが具体的に捉えにくくなり、立式に戸惑う児童が出てきます。
　そこで、立式にあたっては、まず具体的な整数の場合の考えから立式を取り扱い、整数の場合でことばの式をつくり、分数の場合でも同じように立式すればよいという見通しをもたせることが大切です。

［4］分数×分数（教科書p.42〜55）

記事一覧に戻る

アンケート