今知りたい授業のワンポイント

分数でわる計算

■分数でわる計算の仕方

　教科書p.57では、除数が分数である場合の計算の仕方について、除法の性質を用いる方法と面積図を利用する方法を扱っています。

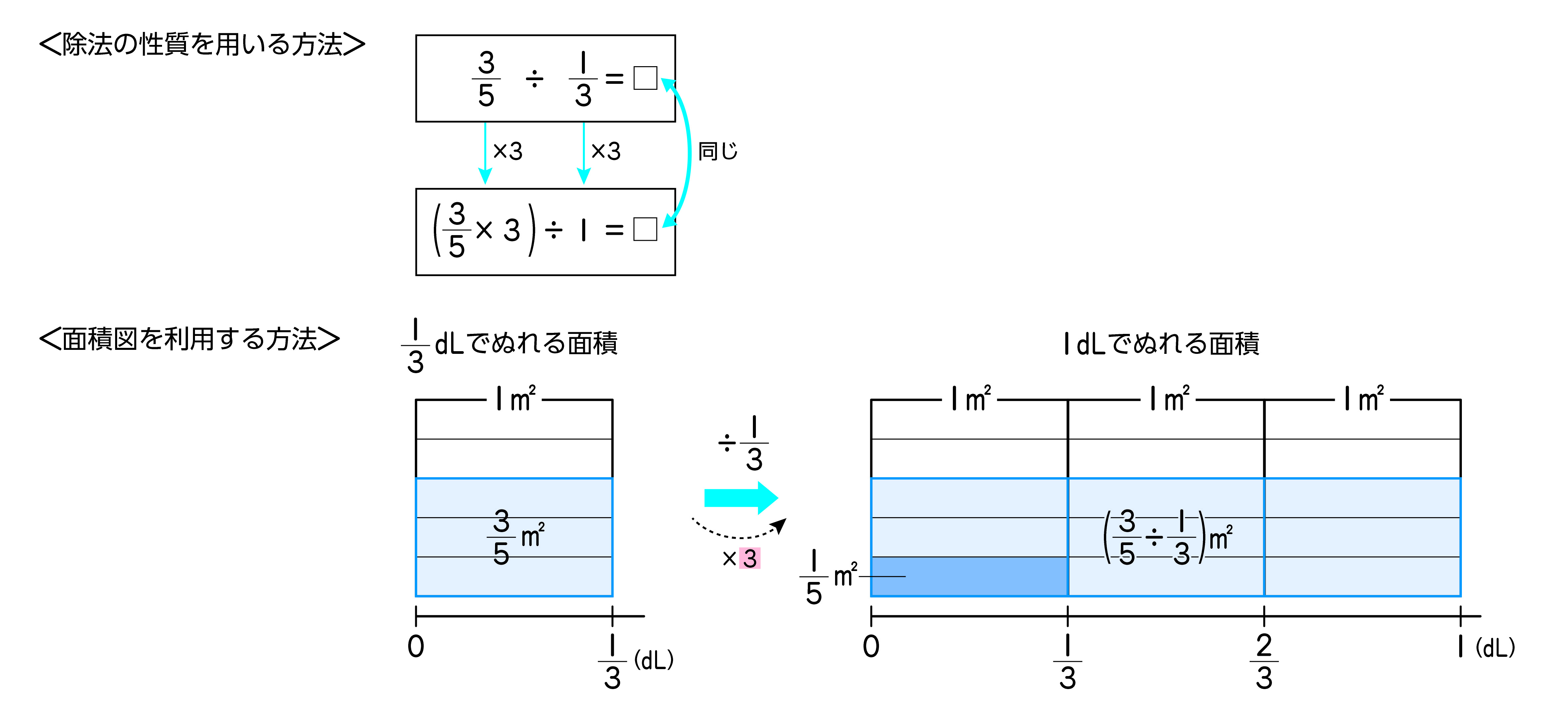
＜除法の性質を用いる方法＞
　除法の性質は、「□÷○＝（□×△）÷（○×△）」（わられる数とわる数の両方に同じ数をかけても商は変わらない）というものです。
　これにより、p.58では、除数が1になる数をかけることで、（分数）÷（分数）の計算を（分数）×（整数）の計算にすることができています。

＜面積図を利用する方法＞
　面積図では、除法の性質を使って導き出した「（分数）÷（分数）＝（分数）×（整数）」の意味をとらえさせるように指導します。

　教科書p.58では、面積図を次のように示すとよいでしょう。
　数直線でペンキの量1/3dLを示します。その上に1m^2の図をかき、横に5等分して3/5m^2がぬられている図を示します。そして、1dLのときの図を示しましょう。数直線をのばし、2/3、1の目盛りをとってペンキの量1dLを示します。その上に3/5m^2がぬられている図を並べかいていきます。ペンキの量、ぬれる面積ともに3倍になっていることをとらえさせます。
　具体的な量のイメージを伴わせながら、計算処理の意味をおさえさせます。

■（分数）÷（分数）の計算の仕方

　一般の分数になった場合、その計算の仕方を面積図で説明するのは難しいことです。
　そのため、除法の性質を使って説明させるとよいでしょう。意味としては、1dLでぬれる面積は2/3dLでぬれる面積の3/2倍であるという理解です。そして、分数のわり算は、逆数をかける計算に帰着できることを理解させます。児童から、面積図を用いる方法が出れば、取り扱ってもかまいません。

［5］分数÷分数（教科書p.56〜69）

記事一覧に戻る

アンケート