今知りたい授業のワンポイント

面や辺の平行と垂直

■面と面

　「5　垂直・平行と四角形」で学習しているように、「平面上の2直線が平行」とは、ある直線にともに垂直に交わる場合を指します。空間内の2平面についても、下の図アのように、ある直線にともに垂直である場合に平行となります。
　平面同士の垂直関係を述べるためには、まず、平面の角を定義する必要があります。例えば、下の図イで2つの平面p、qが直線lで交わっているとします。直線l上に点Aを任意にとり、各平面上でAを通りlと垂直な直線をかきます。この2直線のなす角をPとQの間の角とします。この角が90°（直角）になるとき、2つの平面が垂直であるといいます。
　このように定義するのは困難だと思われるので（中学校で学ぶ内容です。）、教科書p.100のように、「下敷きをまっすぐに立てる」「壁の面にまっすぐついたてを立てる」「包丁で羊羹をまっすぐに切る」などの数学的活動を取り入れ、実感的に理解させることが大切です。具体的に考察させるようにし、抽象的な扱いにならないようにしましょう。

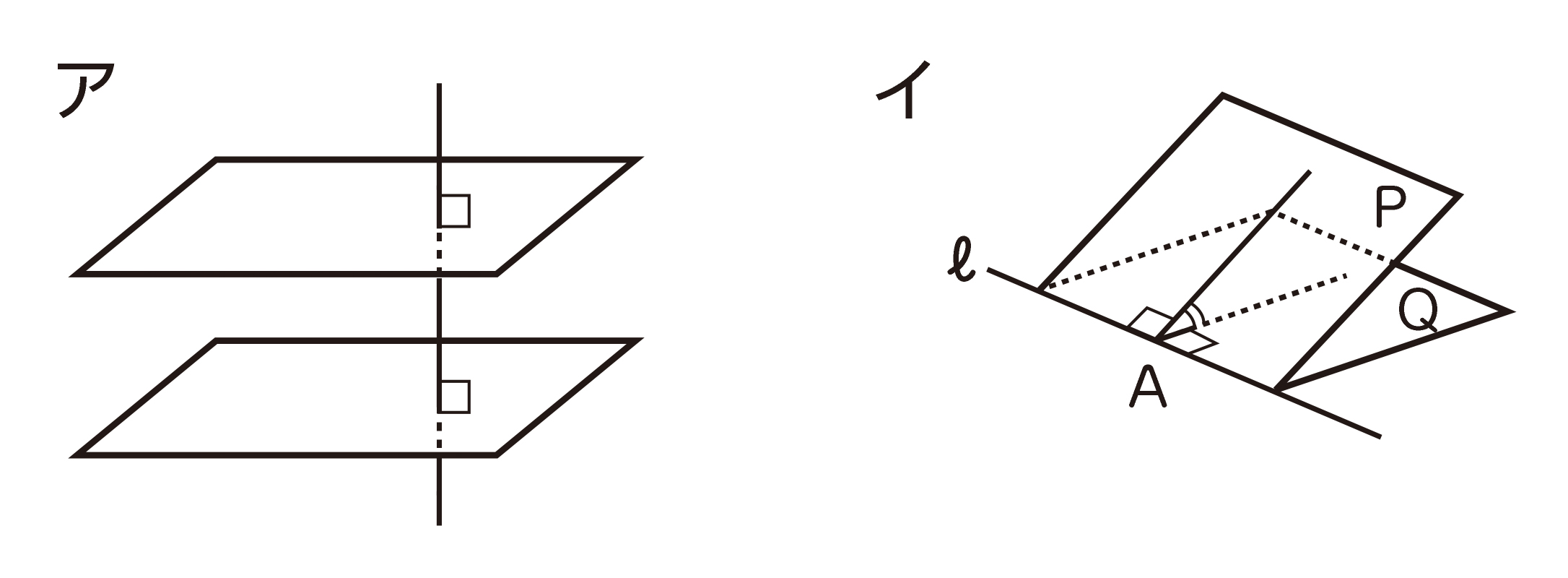
■辺と辺

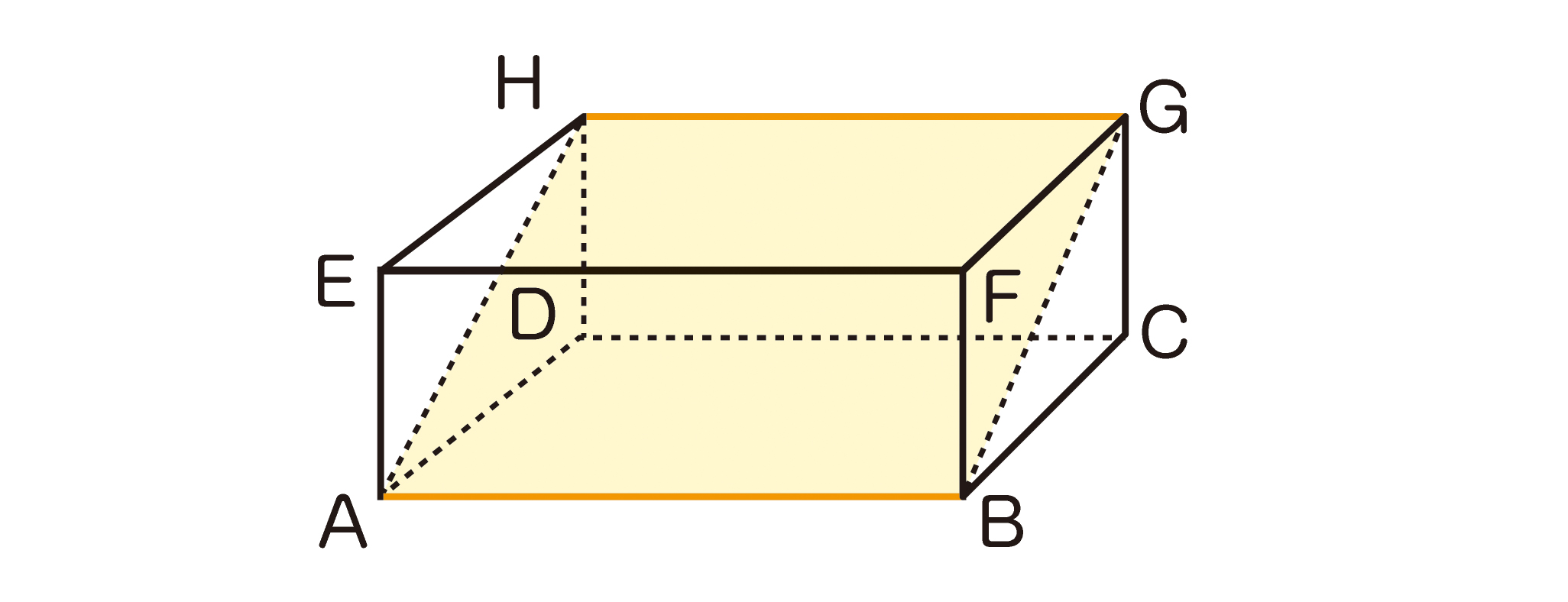
　空間内の2直線が平行であるとは、2直線がある1つの平面に含まれていて交わらないときをいいます。したがって、直方体の1辺に対して、それと平行な辺は3つ存在します。同じ面に含まれる2つの辺については明らかですが、下の図の辺ABと辺HGのように同一平面上にはないものがあります。この場合、直方体を斜めに横断する長方形が存在することを図などを使って捉えさせ、辺の平行について確認させましょう。
　また、下の図で辺ABと辺GFは交わりませんが、平行ではありません。このような場合を「ねじれの位置にある」といいます。これは、中学1年の学習内容です。
　空間内の2直線が垂直であることは、教科書p.101では垂直に交わる場合に限定しています。したがって、直方体の1つの辺に垂直な辺は、その辺の端にそれぞれ2つずつ、計4つあります。

16.直方体と立方体（教科書下巻p.94〜107）

記事一覧に戻る

アンケート