今知りたい授業のワンポイント

かくれた数はいくつ

■逆思考問題の解き方

　教科書p.32〜35で取り扱う3要素2段階の問題のように、逆思考を含むものについては、その数量の関係を、□やxを使った等式に表すことがよくあります。しかし、ここでは、題意に従って逆に考えていく仕方で解かせることをねらいとしているので、その点に注意して指導するようにしましょう。
　ここで特に押さえておきたいことは、線分図が数量の関係や場面を表し、逆の関係を順の関係に置き換えることができる「思考を助ける道具」となること、発表場面においては「説明するための道具」となることを理解させることです。答えさえ合えばよいというのではなく、答えに行きつくまでの思考の過程やその表現を大切にしましょう。

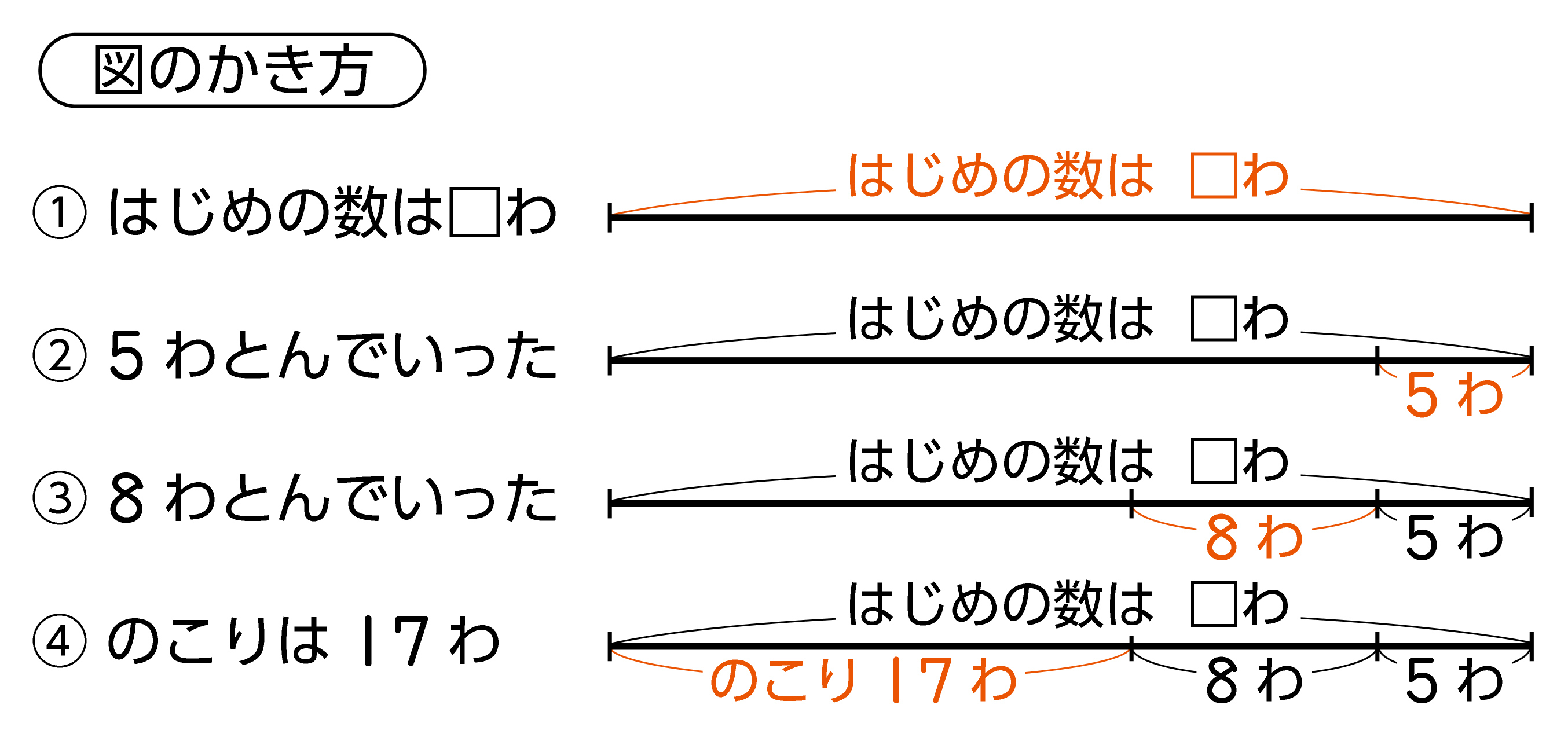
■線分図のかき方

　線分図のかき方の指導にあたっては、第2学年のテープ図のかき方を想起させ、問題文にかかれている内容や要素を1つずつ確かめていくようにさせましょう。
　教科書p.33「図のかき方」（QRコンテンツ）の動画で紹介している線分図のかき方については、次のことに留意したものになっていますが、他のかき方でも児童が納得できれば問題ありません。児童の実態に応じて柔軟に指導するようにしましょう。

・右側に減った数を示している理由
　　線分図は第2学年のテープ図をもとに、テープ図は第1学年のブロック操作をもとにしています。1年生のひき算において、ブロックを右側に取り去る操作で求残を規定していることから、ここでも右側に示しています。

・上側を「はじめの数」としている理由
　　問題文に先に出てきた方を上側にかいています。

・線分の長さについて
　　図をかく時点ではわからない数量があるので、実際の数量の大きさの比と揃える必要はありません。逆に、わかっている数量については揃えたいという児童がいれば認めましょう。

・定規の使用について
　　児童の実態によりどちらでも構いません。

見方・考え方を深めよう「あれ？　たくさんいたのに……」（教科書上巻p.32〜35）

記事一覧に戻る

アンケート