今知りたい授業のワンポイント

およその形と大きさ

■概形を捉えておよその面積を求める

　面積や体積を測定しようとする場合、身の回りの図形は必ずしも基本図形そのものとは限りません。
　そこで、教科書p.190〜191では、曲線や直線で囲まれた図形の求積に取り組んでいます。その際に大切なことは、公式が利用できるシンプルな形とみなすことと、誤差が少なくなるように直線を決めることです。

■概形を捉えておよその体積を求める

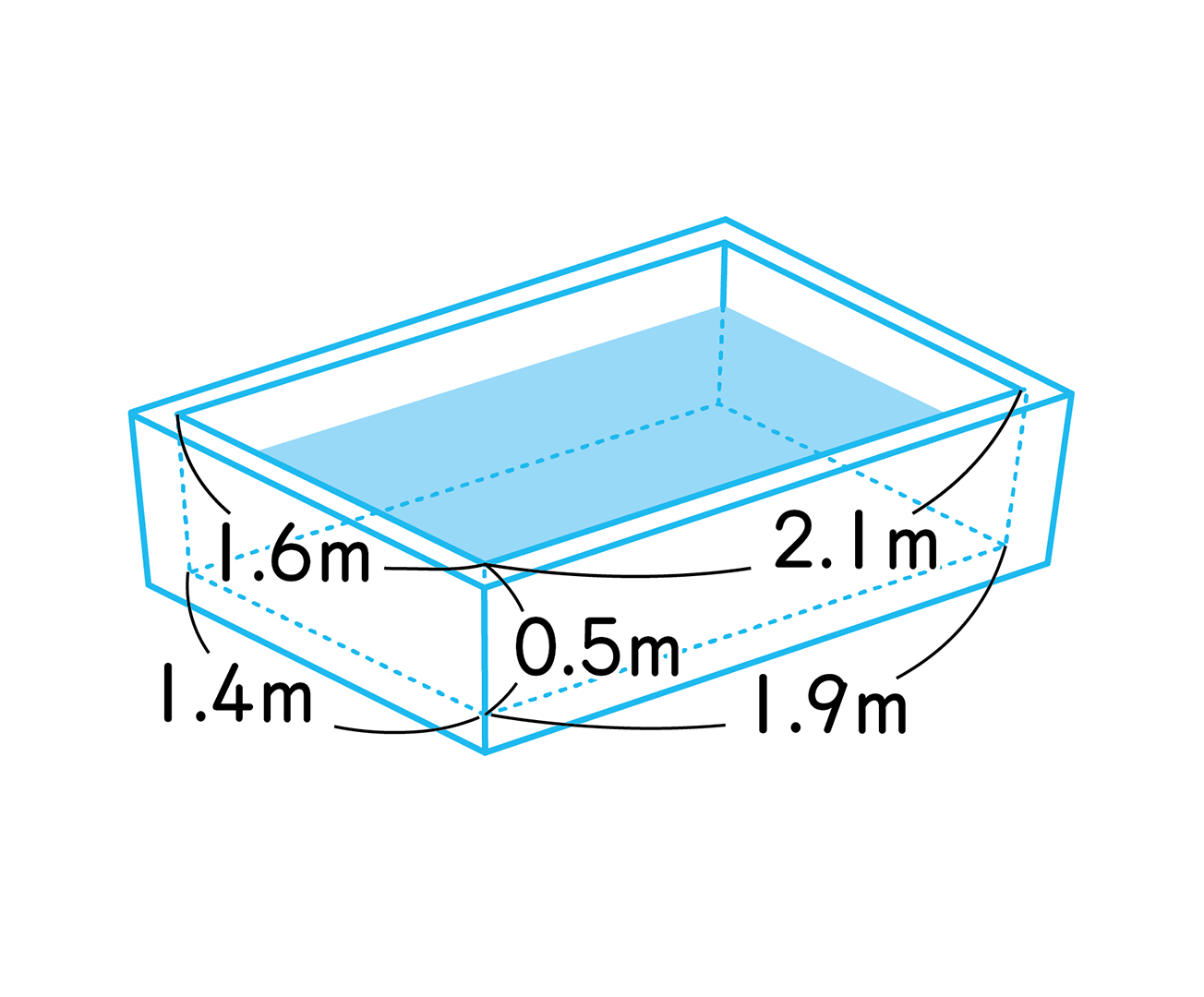
　教科書p.192［2］の浴槽の問題については、概形を直方体と捉えた上で、次の3つのタイプの見積もりが考えられます。
（a）縦1.4m、横1.9m、高さ0.5m
（b）縦1.6m、横2.1m、高さ0.5m
（c）縦1.5m、横2m、高さ0.5m

　概括的に把握して数値化する際には、概形の捉え方によって得られた値に差が出ます。（a）や（b）も誤りではありませんがが、相殺のアイデアを生かすと（c）が最も適切と言えます。
　なお、（a）や（b）での求積では、正確に計算して答えを四捨五入する方法や、計算する前に個々の数を概数にして処理する方法もあります。いずれにしても、およその大きさを求める上で概算や見積もりを活用していることを確認し、測定値や計算の処置について厳密さを問う必要がないことを理解させることが大切です。

13.およその形と大きさ（教科書p.190〜197）

記事一覧に戻る

アンケート