今知りたい授業のワンポイント

関数の考え、関数表のかき方

■関数的な考えの位置づけ

　関数の考えとは、数量や図形について取り扱う際に、それらの変化や対応の規則性に着目して問題を解決していく考えです。特に、伴って変わる2つの数量の関係を考察し、特徴や傾向を表したり、よみ取ったりできるようにすることが主要なねらいです。
　関数の考えを構成する主要な要素には、次の3つがあります。
　1．ある場面で、数量や図形についての事柄が、他のどんな事柄と関係するのかに着目すること（依存関係にある数量に着目すること）。
　2．2つの事柄の変化や対応の特徴を表、式、グラフを使って調べていくこと（変化や対応の規則性をよみ取ること）。
　3．見出した変化や対応の規則性を活用し、その思考過程や結果を表現したり説明したりすること。

■関数表のかき方

　依存関係にある2つの数量を取り出し、その対応の組（順序対）をつくっても、ばらばらな組のままでは、2つの数量にどんな関係があるのかわかりにくいでしょう。そのため、表に整理させる必要があります。
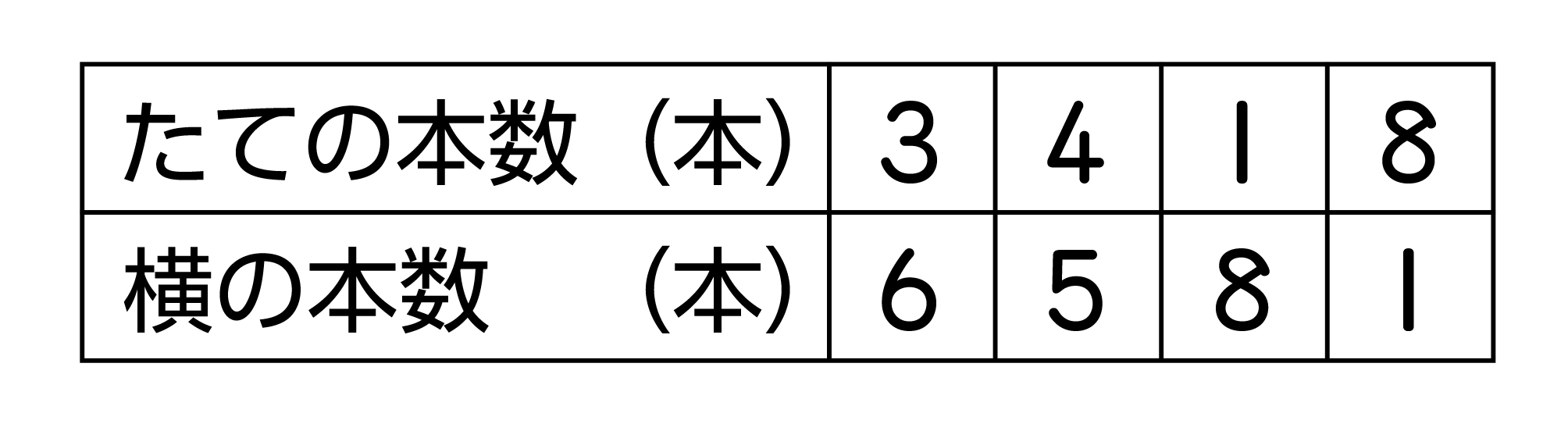
　関数表のかき方は、教科書p.83の通りです。指導のポイントは、表の項目の決め方と、変わり方のわかりやすい表のかき方の2点です。前者について、一般に、表の上段には変わる数（独立変数）をかき、下段には伴って変わる数（従属変数）をかくことを指導します。後者については、変わり方がわかりやすいようにするためには、上段の変わる数を1ずつ規則正しく増やしていき、それに伴って変わる数を下にかかせるように指導します。
　何となく表を書けばよいと思う児童もいます。そこで教師がわざと下のような表を示し、教科書の表と対比させ、1、2、3、…と増やしていくと、変わり方がよくわかることに気づかせるとよいでしょう。

15.変わり方（教科書下巻p.82〜88）

記事一覧に戻る

アンケート