今知りたい授業のワンポイント

分数と小数・整数の関係、分数倍

■分数と小数・整数の関係

　分数と小数との関係では、分数を整数のわり算に戻して、その商を小数の形に表したり（教科書p.126）、小数を分母が、10、100などの分数の形に直したりして（p.127）、相互の関係を理解させます。
　特に、小数は、分母が10、100、1000などの分数を、整数と同じように位取りして小数点を使って表現したものであることを押さえさせましょう。
　0.7＝7/10　　0.13＝13/100　　0.009＝9/1000

　なお、小数を分数に直す方法としては、次の2通りの考え方があります。
　　1．単位小数0.1、0.01、0.001と分数の関係をもとに考えていく方法
　　2．分数の第二義を使う方法　（例）0.7＝7÷10と考えて7/10を導く。

■分数倍について

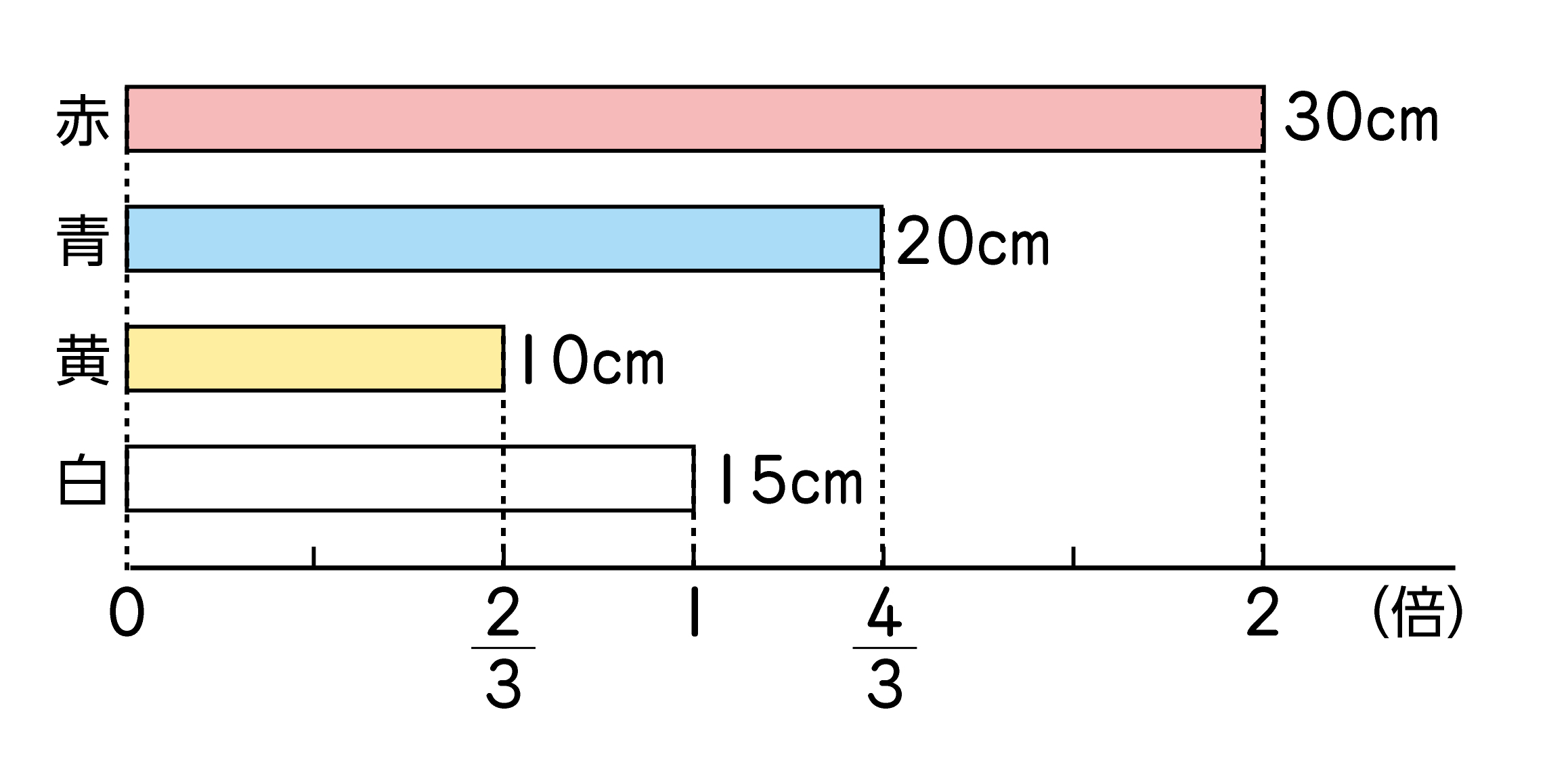
　「整数倍」や「小数倍」と同様に、「倍」を分数で表してもよいことに気づかせるために、テープ図や関係図を有効に活用していきましょう。立式の根拠をこれらの図を使って説明し、答えを計算で求める際に、第9時で学習した▲÷■＝▲/■を想起させ、整数倍や小数倍と同様に「倍」を分数で表してもよいことを理解させます。
　しかし、日常場面では4/3倍というように、分数に倍をつけることはほとんどありません。そのため、児童は、20÷15の商が4/3になることを学習していても、「何倍かにあたるのを表すのに分数を用いてよいだろうか」という疑問をもつ児童も見られることに注意して指導にあたるようにしましょう。
　なお、このときの割合を表す4/3は、「割合分数」と呼ばれる分数です。割合分数については、第6学年で学習することになります。

9.分数（教科書p.114〜131）

記事一覧に戻る

アンケート