今知りたい授業のワンポイント

小数をかけることの意味

■小数をかけることの意味の指導

　これまでに学習してきた乗数が整数の乗法では、（1個分の大きさ）×（何個分）＝（全体の大きさ）として、同数累加で意味を捉えてきました。しかし、この「何個分」にあたる数（乗数）が小数になると累加の考えでは説明できなくなります。例えば、「80×2.3」を「80円の2.3個分」と考えても累加の意味をなさないということです。

　そこで、乗数が小数の場合にも通じるように乗法の意味を拡張する必要があります。それが「○倍」としての解釈です。
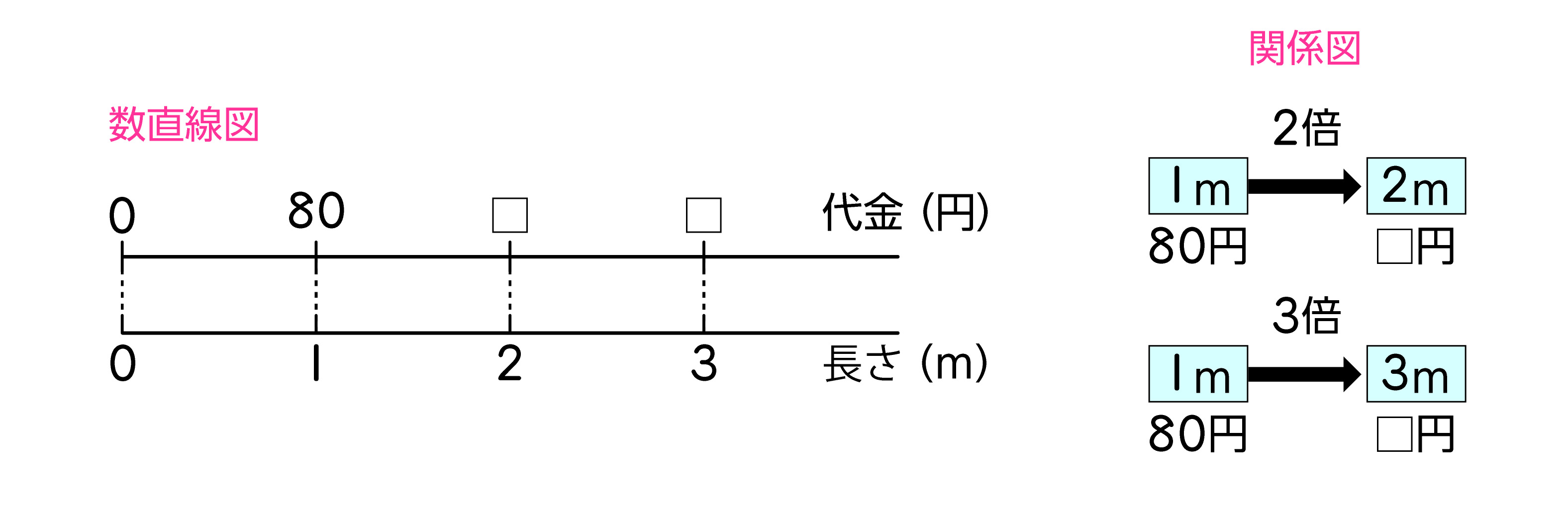
教科書p.34でのねらいは、比例関係を根拠にしながら、数直線図や関係図を用いて、かけ算の演算の意味を、（基準量）×（何倍）と捉え直していくことにあります。

■数直線図を用いること

　教科書p.35では、数直線図や関係図を用いて数量の関係を捉え、「長さと代金は比例しているから、長さが2.3倍になると、それに伴って代金も2.3倍になる。だから、式は80×2.3になる。」と児童が2.3倍の大きさのイメージをもって説明できることを期待しています。
　しかし、この段階での2.3倍の大きさのイメージとは、「2倍の大きさより少し大きいけれど3倍より小さい」「2倍と3倍の真ん中より少し小さい」にとどまります。
　また、数直線図は児童がかいたりよんだり立式の根拠にするには難しく、慣れが必要です。そのためまずは、比例関係をどう表しているかよみ取ることを重視し、次にかくことに繋げるようにします。

　なお、数値が2.3mのような帯小数になっているのは、0.8mのような純小数の場合だと被乗数より積が小さくなるという別のハードルがあるからです。また、2.3mの代金を扱うことで、2mの代金よりも大きく3mの代金よりも小さいというように、整数の場合と関連づけて積を見当づけることができるというよさもあります。

［4］小数のかけ算（教科書p.34〜49）

記事一覧に戻る

アンケート