今知りたい授業のワンポイント

体積

■1cm^3の大きさ

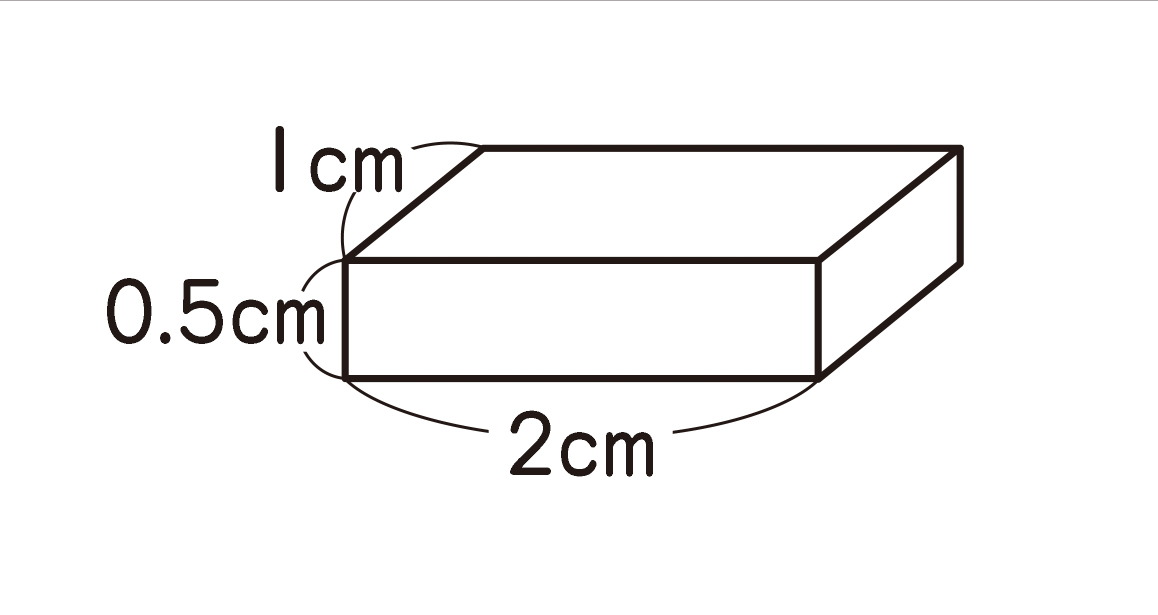
　1cm^3の大きさというと、1辺が1cmの立方体の形だけではありません。下の図のように、縦1cm、横2cm、高さ0.5cmでも、体積は1cm^3になります。1cm^3の代表的な形として、1辺1cmの立方体の体積が考えられるように指導しましょう。
　教科書p.17　1の問題の（あ）（い）の図のように、1辺が1cmの立方体が積み重なっているイメージがしにくい児童や体積を正しく求められない児童には、実際に1辺が1cmの積み木を積み重ねる活動に取り組ませるとよいでしょう。
　なお、実際の指導にあたっては、1辺が1cmの立方体の模型と、粘土で作った立方体の形をいろいろに変えて、体積は変わらないことを捉えさせておくとよいでしょう。

■L字型の図形の体積の求め方の説明

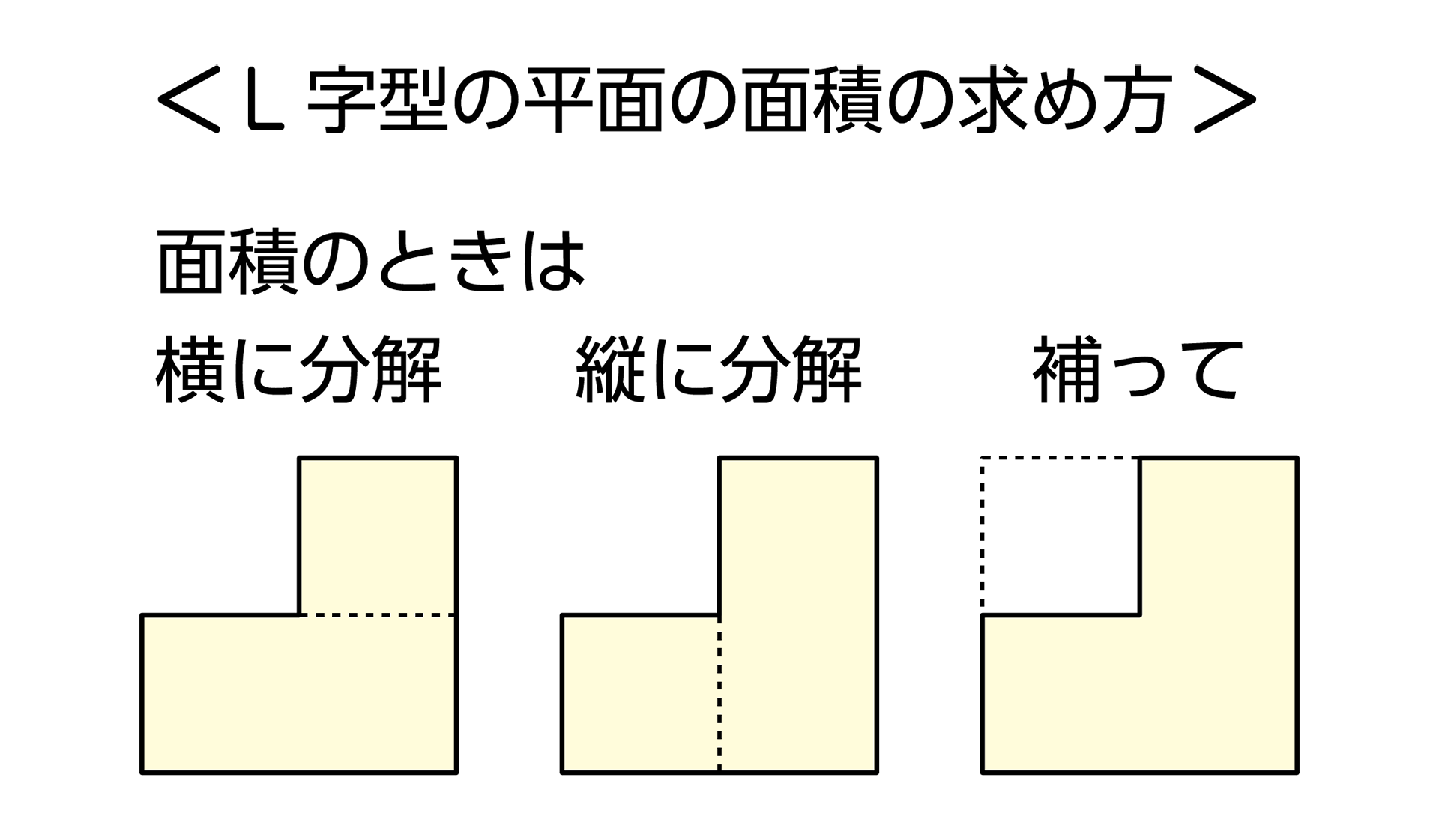
　L字型の平面の面積については、第4学年で、下の図のように正方形や長方形に分解したり、補ったりして、必要な部分の長さを求め、面積の公式を活用して求めました。L字型の図形の体積も、直方体や立方体に分解したり、補ったりして、同様に体積の公式を活用して求めます。つまり、次のように既習事項を活用することがポイントです。

・L字型の面積の学習で、既習の面積の公式を活用したことを想起すること。
・既習の直方体や立方体の体積の公式を活用しようとすること。

　そして、体積の求め方を説明する際には、次のように、言葉、数、式、図を結び付けてわかりやすく説明できるようにしましょう。

・図を使って、L字型をどのように工夫したのかを説明する。
・図を使って、体積を求めるためにどの辺の長さを測ったのかを説明する。
・図を使って、どの部分の体積をどんな式で計算したのかを説明する。


　このように体積の求め方を考え説明する中で、児童のつまずきを的確に捉え、適切に指導することが重要です。児童のつまずきとして、例えば、次のようなことが考えられます。

・求め方を全く思いつかないために、図にかけない。
・求め方はわかるが、図への表現の仕方がわからず困っている。
・図に表現できるが、必要な部分の長さが求められない。
・体積の公式の活用がうまくできない。

　複合立体図形のイメージをもちにくい児童には、2つの箱を組み合わせたり粘土で作ったりした実物を観察させるようにしましょう。表現の仕方で困っている児童には、教科書p.22の（イ）にある図を示し、ゆいさん、かずさん、そらさんの考えた式がどこの体積を求めているかを考えさせるなどの支援をするとよいでしょう。

2.体積（教科書p.16〜29）

記事一覧に戻る

アンケート