今知りたい授業のワンポイント

いくつ分とかけ算

■数図ブロックとかけ算の意味

　算数の内容には、数学的活動として（半）具体物の操作を行うことによって、理解が確かになるものが多く、特に低学年ではその傾向が強くあります。
　［10］かけ算（1）でも、数図ブロックを使った操作活動を重視して、児童がかけ算の意味を理解できるように指導しましょう。
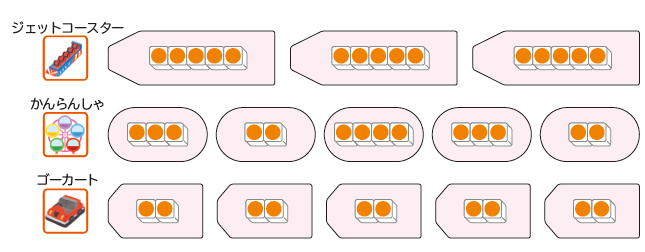
　指導にあたっては、p.5の絵の乗り物をイメージできるような枠の上で数図ブロックを操作させるようにするとよいでしょう。この活動を通して、

ア．「同じ数ずついくつ分」になる場合とそうでない場合の区別
イ．「基準量のいくつ分」という表現

の2点について指導し、かけ算の意味の理解に繋げていくことが大切です。

■2つの事柄からかけ算を定義する

　何かを定義する際、1つの事柄だけを取り上げるのではなく、複数の事柄を取り上げて、それらから見出した共通点やきまりを定義とすることで、児童のより深い理解に繋げることができます。
　教科書p.6では「4×3」を扱っていますが、もし、「4の3つ分（4×3）」だけでかけ算を定義したとすると、それ以外の「○の□つ分（○×□）」という場合もかけ算になるかどうかが定義から捉えられない児童もいるかもしれません。「4の3つ分が4×3」や「3の5つ分が3×5」のように、少なくとも2例で「○×□」が「かけ算」であると定義すれば、どういうときに「かけ算」になるかがより明確になります。

■基準量を明確にする

　教科書p.8では連続量についてのかけ算を扱っています。基準量が何であるのかをしっかりとらえさせましょう。「何のいくつ分」かをつかませ、立式させるようにします。かけ算の答えは、累加で求めさせますが、基準量があいまいにならないように注意しましょう。

［10］かけ算(1)（教科書下巻p.2〜23）

記事一覧に戻る

アンケート